
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема Гаусса-Остроградского
|
|
|
|
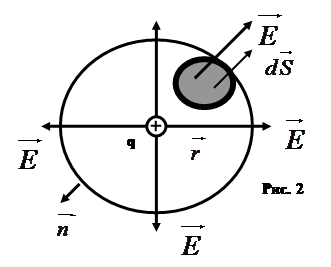 Найдем поток вектора напряженности электрического поля, создаваемого точечным зарядом q, через сферическую поверхность радиуса r.
Найдем поток вектора напряженности электрического поля, создаваемого точечным зарядом q, через сферическую поверхность радиуса r.
Площадь ее поверхности . Силовые линии электрического поля, (см. рис. 2), идут по радиусам к поверхности сферы и поэтому угол между векторами
. Силовые линии электрического поля, (см. рис. 2), идут по радиусам к поверхности сферы и поэтому угол между векторами 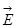 и
и  равен нулю.
равен нулю.
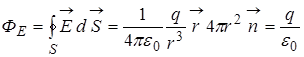 . (4)
. (4)
Можно показать, что поток через замкнутую поверхность не зависит от формы поверхности и от расположения зарядов в ней.
Рассмотрим поток, создаваемый системой зарядов, сквозь замкнутую поверхность произвольной формы, внутри которой они находятся (рис.3): 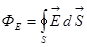 .
.
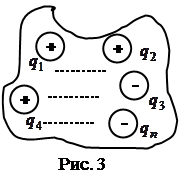 Согласно принципу суперпозиции
Согласно принципу суперпозиции  поэтому
поэтому
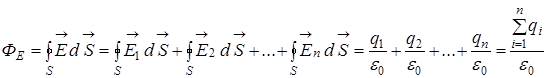 таким образом
таким образом 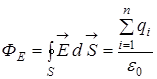 . (5)
. (5)
Итак, мы доказали теорему Гаусса — Остроградского:
«полный поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на 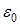 ».
».
Теорему Гаусса — Остроградского, (5), можно записать в дифференциальной форме:

 , (6)
, (6)
где 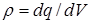 - объемная плотность заряда.
- объемная плотность заряда.
 , знак
, знак 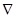 - оператор набла.
- оператор набла.
Из теоремы Гаусса — Остроградского вытекают следствия: 1) линии вектора  (силовые линии) нигде, кроме зарядов, не начинаются и не заканчиваются: они, начавшись на заряде, уходят в бесконечность для положительного заряда, либо, приходя из бесконечности, заканчиваются на отрицательном заряде (картина силовых линий приводится на рис. 4); 2) если алгебраическая сумма зарядов, охватываемых замкнутой поверхностью, равна нулю, то полный поток через эту поверхность равен нулю; 3) если замкнутая поверхность проведена в поле так, что внутри нее нет зарядов, то число входящих линий вектора напряженности равно числу выходящих и поэтому полный поток через такую поверхность равен нулю.
(силовые линии) нигде, кроме зарядов, не начинаются и не заканчиваются: они, начавшись на заряде, уходят в бесконечность для положительного заряда, либо, приходя из бесконечности, заканчиваются на отрицательном заряде (картина силовых линий приводится на рис. 4); 2) если алгебраическая сумма зарядов, охватываемых замкнутой поверхностью, равна нулю, то полный поток через эту поверхность равен нулю; 3) если замкнутая поверхность проведена в поле так, что внутри нее нет зарядов, то число входящих линий вектора напряженности равно числу выходящих и поэтому полный поток через такую поверхность равен нулю.
Теорема Гаусса позволяет рассчитать электрические поля, создаваемые заряженными телами различной формы:
2.2.1.Поле равномерно заряженной, бесконечно протяженной плоскости (рис. 5).
Построим цилиндр, ось которого перпендикулярна к поверхности, и применим теорему Гаусса-Остроградского

 ,
,
т.к.  ,
,
то 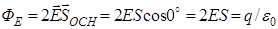
отсюда 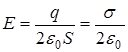 , (7)
, (7)
где s = q/S поверхностная плотность заряда, измеряемая в СИ в Кл/м2.
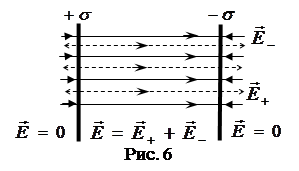 2.2.2. Поле между двумя бесконечно протя ж енными, разноименно заряженными параллельными плоскостями, (см. рис. 6). Вне внутреннего промежутка,
2.2.2. Поле между двумя бесконечно протя ж енными, разноименно заряженными параллельными плоскостями, (см. рис. 6). Вне внутреннего промежутка,  = 0 т. к. поля, созданные разноименно заряженными параллельными пластинами, направлены противоположно друг другу; между плоскостями
= 0 т. к. поля, созданные разноименно заряженными параллельными пластинами, направлены противоположно друг другу; между плоскостями 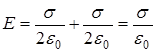 .
.
Итак:  . (8)
. (8)
По этой же формуле определяется напряженность электрического поля вблизи заряженного проводника.
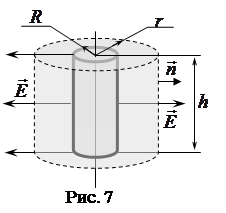 2.2.3. Поле заряженного цилиндра: заряженный цилиндр радиуса R, (см. рис. 7), окружим коаксиальной цилиндрической поверхностью радиуса r; поток вектора
2.2.3. Поле заряженного цилиндра: заряженный цилиндр радиуса R, (см. рис. 7), окружим коаксиальной цилиндрической поверхностью радиуса r; поток вектора  через основания равен нулю, т. к.
через основания равен нулю, т. к.  , где
, где 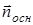 – внешняя нормаль к основаниям цилиндра; поток через боковую поверхность
– внешняя нормаль к основаниям цилиндра; поток через боковую поверхность  , здесь h – высота цилиндра. Согласно теореме Гаусса – Остроградского, при
, здесь h – высота цилиндра. Согласно теореме Гаусса – Остроградского, при 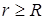

 , (9)
, (9)
где t = q/ h — линейная (погонная) плотность заряда, которая измеряется в Кл/м. Когда r < R, то  = 0.
= 0.
2.2.4 Поле заряженной сферы: поток вектора  через поверхность сферы радиуса r,
через поверхность сферы радиуса r,

 (см. рис. 8, вверху), которая окружает заряженную сферу, имеющую радиус R,при r
(см. рис. 8, вверху), которая окружает заряженную сферу, имеющую радиус R,при r 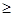 R
R 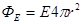 . По теореме Гаусса – Остроградского
. По теореме Гаусса – Остроградского
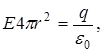 oткуда
oткуда  (10)
(10)
|
при r < R имем  = 0. Это свойство используют для экранировки от полей внешних зарядов; график Е = f(r) для случая заряженной сферы приведен на рис. 8, внизу.
= 0. Это свойство используют для экранировки от полей внешних зарядов; график Е = f(r) для случая заряженной сферы приведен на рис. 8, внизу.
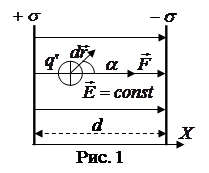 Лекция 3. Потенциал электрического поля
Лекция 3. Потенциал электрического поля
3.1. Работа сил электрического поля:
 на расстояние d:
на расстояние d:
 ,
, 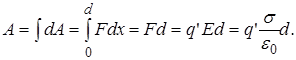
Таким образом, работа, совершаемая силами поля, не зависит от формы пути, по которому перемещался заряд, а зависит только от расстояния d, измеряемого вдоль силовой линии между начальным и конечным положением заряда.
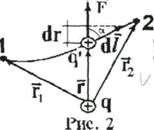 3.1.2. В неоднородном поле точечного заряда q (см. рис. 2) Найдем работу по перемещению пробного заряда
3.1.2. В неоднородном поле точечного заряда q (см. рис. 2) Найдем работу по перемещению пробного заряда 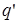 из точки 1 в точку 2 в поле, создаваемом точечным зарядом q:
из точки 1 в точку 2 в поле, создаваемом точечным зарядом q:

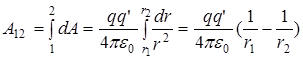 . (2)
. (2)
И в этом случае работа сил не зависит от формы пути. Она является только функцией начального и конечного положения заряда.
Для замкнутой траектории L она равна нулю, т. к.  , т. е.
, т. е.
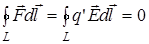 или
или 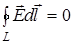 , (3)
, (3)
т.е. ЦИРКУЛЯЦИЯ ВЕКТОРА НАПРЯЖЕННОСТИ ПО ЛЮБОМУ ЗАМКНУТОМУ КОНТУРУ РАВНА НУЛЮ.
В механике было приведено следующее определение: «Силы, работа которых не зависит от формы пути, называются консервативными силами, а поля, работа сил которых не зависит от формы пути, называются потенциальными полями». Таким образом, рассмотренное нами электростатическое поле является потенциальным, а кулоновские силы - консервативными.
|
|
|
|
|
Дата добавления: 2014-10-23; Просмотров: 1821; Нарушение авторских прав?; Мы поможем в написании вашей работы!