Наблюдаемость

Наблюдаемость систем управления.

Рассмотрим линейные системы, динамика которых описывается дифуранением n – порядка. В этом случае состояние системы будет определятся n – координатами. Эти координаты состояния системы не обязательно будут совпадать с физическими величинами, в т.ч. и с выходными координатами.

Система может описываться через входные и выходные величины или через координаты состояния.

В общем случае обозначение выходной управляющей величины через y от 1 до q.

Входные координаты обозначаются через U от 1 до m.

В качестве системы можно рассмотреть либо замкнутую САУ, тогда координаты U будут играть роль задающих воздействий G.

Либо сложно управляемые объекты, тогда величина U будет являться управляющим воздействием со стороны регулятора. Уравнение динамики линейной системы можно представить в виде:

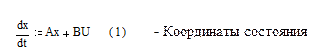
c = cx (2) – в такой записи х – координата состояния системы.

Непосредственно наблюдается величинами, являющимися выходными величинами y, которые можно измерить.

Наблюдаемостью системы - называют такое её свойство, когда путём её наблюдения или измерения её выходные величины y(t) при заданных входных управлениях U(t) на интервале времени 0 £ t ³ T можно определить все координаты начального состояния системы х. В этом случае система будет полностью наблюдаемой.

Система будет не полностью наблюдаемой если через измерение выходной величины определяются не все координаты начального состояния системы.

Пусть система уравнений задана в формуле (1) и (2). Следуя теореме Калмана составляем матрицу n*nq.

Матрица имеет вид. Н = [C^T |A^TC^T |(A^T)²C^T| …| (A^T)^n-1C^T]

Система будет полностью наблюдаемой если ранг матрицы Н будет = n. n – порядок матрицы А.

Система будет не полностью наблюдаемой если ранг матрицы Н r<n. Можно выделить наблюдаемую часть которая будет иметь порядок r. В том случае, когда имеется одна измеряемая величина y матрица С будет иметь одну строку, а транспортируемая матрица – один столбец.

Для полной наблюдаемости требуется чтобы матрица состояла из одних нулей.

С точки зрения управляемости и наблюдаемости нельзя в передаточных функциях сокращать одноимённые сомножители и переставлять сомножители местами.

Дата добавления: 2014-10-23