Исследование автоколебаний с помощью гармонической линеаризацией

Автоколебания нелинейных САУ. Определение параметров автоколебаний.

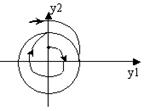
В нелинейной САУ в зависимости от значений начальных отклонений процессы могут быть: расходящийся колебательный (3) или сходящийся колебательный (2).

Автоколебания в НСАУ являются собственными, т.е существуют при возмущении f = 0 и в тоже время это свободные автоколебания. Частота и амплитуда зависит от параметров системы.

Если в реальной системе существуют автоколебания следовательно существует нелинейность в этой системе.(дыхание, часы, работа сердца)

Автоколебательная система – та система которая способна создавать незатухающие колебания. Она характеризуется существованием 3-х свойств:

1.Источник питания.

2.Клапан или вентиль, регулирующий поступающую энергию в систему.

3.ОС с колебательной системы на клапан.

Аналитический метод, используется при исследовании НСАУ.

Сущность метода – отыскание периодического решения на входе нелинейного элемента с последующим разложением сигнала на его выходе в ряд Фурье и замена выходного сигнала его первой гармоникой.

Эта замена справедлива если система является фильтром низких частот, т.е. если система подавляет все высшие гармоники.

Позволяет решить 2 задачи:

1.Выявить автоколебания в НСАУ.

2.Найти параметры автоколебаний (амплитуду и частоту)

Выявление автоколебаний:

1-й этап решения – осуществление гармонической линеаризации, т.е. замена нелинейной статической характеристики эквивалентной передаточной функцией.

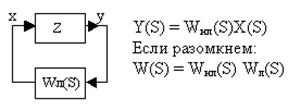
Эта система линейна лишь для фиксированных значений a и w_а.

Искомые значения амплитуды и частоты входящие а W_л(S) соответствуют наличию в системе незатухающих колебаний, т.е. эти параметры могут быть найдены, если известны условия, при которых система находится на границе устойчивости. Для определения границы устойчивости можно использовать существующие критерии устойчивости для линейных САУ.

Критерий Найквиста: Если разомкнутая цепь системы устойчива, то для устойчивости замкнутой системы н. и д. чтобы АФЧХ разомкнутой цепи не охватывала точку с координатами (-1; j0).

Критерий Раусса - Гурвица позволяет определять устойчивость системы по коэффициентам хар. урав-ия.

Необходимым условием устойчивости явл. положительность всех коэф. хар. ур-ия.

a₀>0, a₁>0 … a_n>0.

Критерий Михайлова. Это частотный критерий и он позволяет судить об устойчивости замкнутой системы.

D(λ) = a₀*λⁿ + a₁*λ^{n -1} +…+ a_{n -1}*λ + a_n . Считать все коэффициенты характеристического уравнения положительными.

Выбор критерия устойчивости зависит от конкретной системы.

Находятся зависимости а = f(T); w_a = f(T)

В нелинейной САУ нахождение границ устойчивости сложнее, т.к. " отклонение а и w_а требует пересмотра W(S) следовательно используют приближенный метод (графический)

Дата добавления: 2014-10-23