Импульсные системы управления

Дискретные системы управления. Классификация.

К дискретным системам относятся – импульсные, цифровые и релейные.

В импульсных системах производится квантование сигнала по времени.

В релейных осуществляется квантование по уровню.

В цифровых и по времени и по уровню.

Для описания дискретных систем используются разностные уравнения.

Дискретные системы отличаются от обычных систем, тем, что в их состав помимо обыкновенных звеньев входят звенья осуществляющие одно или несколько квантований.

Линейная импульсная система состоит из одного или нескольких элементов и непрерывной части.

Для описания дискретных сигналов применяют решётчатую функцию.

НЭ – импульсный элемент.

Для импульсных систем в основном применяют 3 вида квантования сигнала по времени:

1. амплитудно-импульсная модуляция (амплитуда импульса ~ входному сигналу)

2. Широтно-импульсная модуляция (широта импульса ~ входному сигналу)

3. Фазоимпульсная модуляция (фаза импульса ~ входному сигналу)

Во всех случаях период чередования импульсов является постоянным

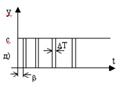
В случае амплитудно-импульсной модуляции (рис б) длительность каждого импульса постоянна, имеет одинаковое значение и обозначается g^Т (0 < g < 1). Амплитуда импульсов принимает значения x[nT]

g = tим / T – скважность

Для единичного импульса, помещённого в начало координат и имеющего длительность gТ можно записать

S1(t) = 1(t) – 1(t - gT)

Выходная величина импульса будет определятся значением x[nT].

Аргумент (t - nT) означает сдвиг каждого импульса на величину nT

от начала координат.

В случае широтно-импульсной модуляции изменяется ширина импульса.

g_n = ax[nT]

g_nT – не должна превышать значение периода Т. аМ £ 1, |х(t)| < М

Величина импульса с остается постоянной и для “+” и для ”-”.

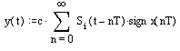
S1(t) = 1(t) – 1(t - g_nT) – широтно-импульсная модуляция.(рис. г)

Фазоимпульсная модуляция.

При фазоимпульсной модуляции амплитуда импульса с и длительностью gТ остаются постоянными. При этом вводится переменный сдвиг импульса по времени относительно каждого периода.

b_n = ах[nT] aM £ 1 - g

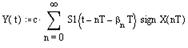
В цифровых системах управления к квантованию по времени добавляется ещё и квантование по уровню. Если обозначим за h – размер одной ступеньки квантования по уровню, тогда величина каждого значения решётчатой функции будет представляться числом ступеней: y[nT] = k*h*sign x[nT]

k – число ступеней h (целое)

Значение решётчатой функции y[nt] запоминается на весь период квантования.

Рассмотрим импульсную систему с амплитудно-импульсн. модуляцией.

Разомкнем эту систему и расчленим условно импульсный элемент на 2 части:

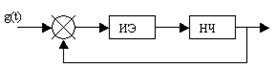
┴(идеальный квантователь) - дает решетчатую ф-ию, определенную в дискретный момент времени nT

S₁(t) придает каждому импульсу Передаточ. и решетчатой функции определенную длительность

Импульсные системы описываются разностными уравнениями: Δf[n] =f[n+1] – f[n] – первая разность решетчатой функции. Первая разность от Δf[n] называется разностью 2-го порядка или второй разностью:

Δ²f[n] =Δf[n+1] – Δf[n] Δ^kf[n] =Δ^k-1f[n+1] – Δ^k-1f[n] – разность произвольного порядка.

Всякое соотношение, связывающее решетчатую функцию f[n] и её разности до некоторого порядка «k» называются разностными урав-ми.

Передаточная функция разомкнутой цепи импульсной системы – это отношение выходной величины к входной при нулевых начальных условиях.

W^*(q, ε) = .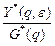

В общем случае перед. ф-ия импульсной цепи

W^*(q, ε) =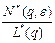

В соответствии со свойствами D-преобразований, передаточная ф-ия W^*(q, ε) будет периодической вдоль мнимой оси.

q = α + jώ

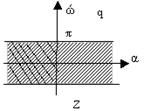т.к. ф-ия периодическая, то она будет определятся в полосе -π< ώ > π, -∞<α>∞, ω=ώt – относительная частота

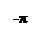Передаточная ф-ия м.б. найдена и через Z-преобразования:

z=e^q (6),

W^*(Z, ε) =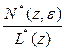

Преобразование (6) отображает основную полосу -π< ώ > π на плоскости z, причем отрезок мнимой оси q=jώ в интервале -π< ώ > π отображается в окружности единичного радиуса z=e^jώ, а левая часть этой полосы отображается – внутрь круга.

X₁ = a*sinωt X₂ = a*sin2ωt t=nT

АФЧХ разомкнутой импульсной системы определяется аналогично обыкновенной линейной системе:

W(S)→W(jω) g(t)=sinωt

Q=ST g[n]=sinώn n=t/T ώ=ωt

W^*(jώ,ε)=W^*(q, ε) – для импульсной системы.

По аналогии с непрерывными системами:

A^*(ώ,ε) = │W^*(jώ,ε)│ φ^*(ώ,ε) = argW^*(jώ,ε)

23. Нелинейные системы управления. Второй метод Ляпунова.

С т. зрения передачи и преобразования сигнала НЛ отлич. от линейных систем тем, что мгновенный коэфффициент передачи зависит от значения входного сигнала. САУ, содержащие звенья, динамика которых описывается НЛ дифференц. уравнениями относят к НЛ системам.

НС-динамика к-х описывается нелин-ми диф ур-ми, это сис-мы, имеющие нелинейную стст-ю хар-ку.

Систему можно представить в виде соединения из 2-х элементов:

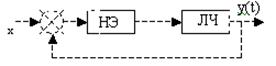
можно свести к:

ЛЧ описывается обычными диф ур-ми с пост-ми коэфф-ми.

НЭ является безинерционным и его выходная величина и вход. величина связаны связаны между собой НЛ алгебраическим уравнением. Нелинейность обусловлена нелинейностью статической характеристики одного из элементов системы.

Нелин-е стат-ие хар-ки делятся на жесткие и гибкие.

Гибкие (не имеющие изломов)

Жесткие (к-ые апроксимирыются кусочно-линейными ф-ми)

1. звено с насыщением
2. звено с зоной нечув-ти
3. звено с мертвым ходом (люфт)
4. Релейные хар-ки.

Теория устойчивости нелинейных систем впервые была предложена Ляпуновым.

Невозмущенное движение устойчиво, если при достаточно малых нелинейных возмущениях, вызванное им возмущенное движение сколь угодно мало отличается от невозмущенного. При этом движение асимптотически устойчиво, если при t→∞ возмущенное движение→к невозмущенному.

Под невозмущ. движением Ляпунов понимал любой, интересующий нас в отношении устойчивости режим работы системы. Невозмущ. движению в фазовом пространстве соответствует начало координат. Этим режимом м. б. как установившийся статический или динамический, так и не установившийся. В качестве возмущения Ляпунов понимал только ненулевые нач. условия.

Ляпунов разработал 2 метода исследования нелинейных систем:

1метод применим только для исследования устойчивости в малом систем, т.е. к системам, к которым полностью применима линейная теория. Линейная система получается в результате линеаризации НЛ системы. Когда линеаризованная система находится на границе устойчивости, то об устойчивости исходной НЛ системы ничего нельзя сказать (м.б. устойчива или неустойчива, в зависимости от вида нелинейности).

2 метод – «прямой» метод. Достаточное условие сходимости: возмущенное движение асимптотически устойчиво, если можно указать такую знакоопределен. ф-ию V(ф-ия, которая при всех значениях переменной имеет один и тот же знак, а в нач. коорд. превращ. в ноль), производная от которой по t, определенная на основании диф. уравнения системы, так же явл. знакоопределен. функцией, но противоположного знака.

Знакоопределенной назыв-ся ф-ия, к-ая при всех знач-х переменных имеет один один знак, а в начале координат обращается в нуль.

Дата добавления: 2014-10-23