Приклад. Параметризація моделі з автокорельованими залишками

Параметризація моделі з автокорельованими залишками

Параметри моделі з автокорельованими залишка­ми можна оцінити на основі чотирьох методів:

1. Ейткена (УМНК);

2. Перетворення вихідної інформації;

3. Кочрена – Оркатта;

4. Дарбіна.

Перші два методи доцільно застосовувати тоді, коли залишки описуються авторегресійною моделлю першого порядку.

Ітераційні методи Кочрена – Оркатта і Дарбіна можна застосо­вувати для оцінки параметрів економетричної моделі також тоді, коли залишки описуються авторегресійною моделлю вищого порядку.

На основі двох взаємопов'язаних часових рядів про роздрібний то­варообіг і доходи населення побудувати модель, що характеризує за­лежність роздрібного товарообігу від доходу, перевірити автокореляцію залишків.

Вихідні дані наведено в таблиці 6.1.

Таблиця 6.1

Дані до задачі (млн.. грн.)

Рік	Товарообіг	Дохід
	25,5	27,6
	26,4	27,4
	27,9	28,7
	28,1	29,5
	28,8	30,9
	29,3	31,4
	29,8	31,8
	30,7	32,2
	31,5	33,6
	32,4	34,7

Розв'язання

1. Ідентифікуємо змінні моделі: залежна змінна 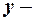роздрібний товарообіг, незалежна змінна 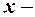дохід населення.

2. Специфікуємо модель у лінійній формі: .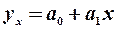

3. Визначимо 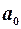, на основі МНК, припустивши, що залишки некорельовані:

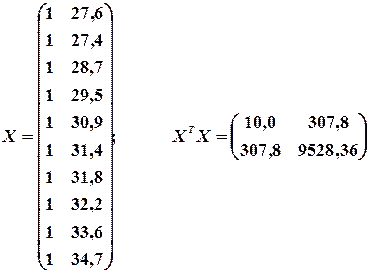
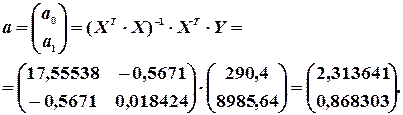
Отже, модель має вигляд:

.

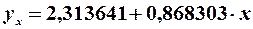4. Знайдемо оцінені значення товарообігу 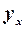на основі отриманої моделі та визначимо залишки .

Таблиця 6.2

Допоміжні розрахунки

Рік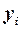
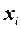
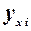
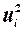
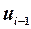
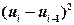
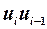
	25,5	27,6	26,27880	-0,77880	0,60653
	26,4	27,4	26,10514	0,29486	0,08694	-0,77880	1,15275	-0,22964
	27,9	28,7	27,23393	0,66607	0,44365	0,29486	0,13779	0,19640
	28,1	29,5	27,92857	0,17143	0,02939	0,66607	0,24467	0,11418
	28,8	30,9	29,14420	-0,34420	0,11847	0,17143	0,26587	-0,05900
	29,3	31,4	29,57835	-0,27835	0,07748	-0,34420	0,00434	0,09581
	29,8	31,8	29,92567	-0,12567	0,01579	-0,27835	0,02331	0,03498
	30,7	32,2	30,27299	0,42701	0,18234	-0,12567	0,30545	-0,05366
	31,5	33,6	31,48861	0,01139	0,00013	0,42701	0,17274	0,00486
	32,4	34,7	32,44375	-0,04375	0,00191	0,01139	0,00304	-0,00050
Сума	290,4	307,8	290,4	0,00000	1,56263	0,04375	2,30996	0,10343

5. Обчислимо оцінку -статистики Дарбіна­­ –Уотсона:

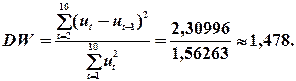
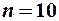Задамо і при та 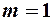знайдемо за таблицею значень -статистики Дарбіна­–Уотсона критичні значення критерію:

– нижня межа – верхня межа

Оскільки 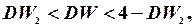то з похибкою щонайбільше у 5% ви­падків можна стверджувати, що автокореляція залишків відсутня.

6. Перевіримо автокореляцію за­лишків моделі на основі критерію фон Неймана.

Обчислюємо фактичне значення критерію фон Неймана:

Звідси .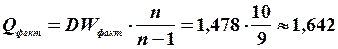

Таб­личне значення критерію фон Неймана при рівні значущості 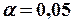і заданій кількості спостережень : .

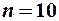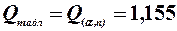Так як , то автокореляція залишків відсутня.

Дата добавления: 2014-10-23