Узагальнений метод найменших квадратів

Розглянемо детальніше загальний випадок оцінювання параметрів моделі з гетероскедастичними залишками.

Запишемо узагальнену багатофакторну регресійну модель у мат­ричному вигляді

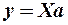(5.8).

Нехай виконуються всі припущення класичної лінійної багатофакторної моделі, за винятком припущення про гомоскедастичність похибок. Якщо до моделі (5.8) застосувати звичайний МНК, от­римана оцінка параметрів буде незміщеною, обґрунтованою, однак не ефективною (не має найменшої дисперсії серед незміщених оці­нок).

За наявності гетероскедастичності для оцінювання параметрів моделі доцільно застосувати узагальнений метод найменших квад­ратів (метод Ейткена), вектор оцінювання якого має вигляд

(5.9).

Вектор 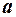містить незміщену лінійну оцінку параметрів моделі, яка має найменшу дисперсію і матрицю коваріацій:

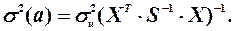
Для отримання УМНК-оцінок необхідно знати коваріаційну матрицю 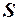вектора похибок, яка на практиці дуже рідко відома. Тому природно спершу оцінити матрицю 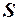, а потім застосу­вати її оцінку у формулі (5.9). Цей підхід є суть узагальненого ме­тоду найменших квадратів.

Визначення матриці 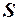. Оскільки явище гетероскедастичності пов'язане лише з тим, що змінюються дисперсії залишків, а коваріація між ними відсутня, то матриця 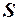має бути діагональною, а саме

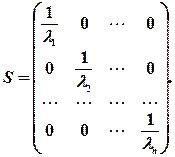
Зазначимо, що матриця 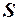залежить від специфічної форми гетероскедастичності й може бути розрахована виходячи з припу­щень про залежність похибок від однієї із незалежних змінних.

У матриці 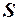значення 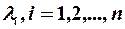можна обчислити, користу­ючись гіпотезами:

1) 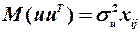, тобто дисперсія залишків пропорційна до змін пояснюючої змінної ;

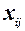2) 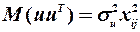, тобто дисперсія залишків пропорційна до зміни квадрата пояснюючої змінної ;

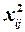3) 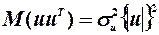, тобто дисперсія залишків пропорційна до зміни квадрата залишків за модулем.

Для першої гіпотези 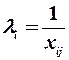. Для другої гіпотези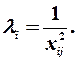

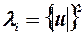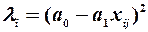Для третьої гіпотези , або , або .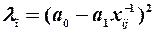

Оскільки матриця 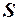симетрична і додатно визначена, то при 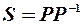матриця 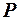має вигляд

, .

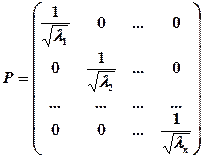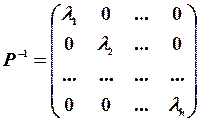Зауваження. Коефіцієнт детермінації не може бути задовільною мірою якості моделі в разі застосування УМНК (на відміну від кла­сичної моделі). У загальному випадку значення коефіцієнта детермі­нації навіть не повинно перебувати в інтервалі [0,1], а додавання чи вилучення незалежної змінної (фактора) не обов'язково зумовлює його збільшення або зменшення.

Основні висновки щодо наявності гетероскедастичності в регресійній моделі

Якщо виявлено гетероскедастичність, а дисперсії невідомі, не­обхідно трансформувати початкову модель з метою усунення гетеро­скедастичності.

Якщо відомі (що, взагалі, рідкість), то невідомі параметри регресійної моделі розраховуються за МНК.

Якщо невідомі, але відомий вигляд залежності між та однією із незалежних змінних 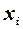, то параметри регресійної моделі розраховуються за УМНК.

Важливим є припущення про нормальний закон розподілу випадкової змінної 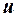. Якщо це припущення порушується (або, як часто буває на практиці, ігнорується), то оцінки параметрів залишають­ся найкращими, однак ми не можемо визначити їх статистичну значущість (надійність) за допомогою класичних тестів значущості (тощо), оскільки ці тести базуються на нормальному законі роз­поділу.

Контрольні запитання

1. Яке явище називається гомоскедастичністю?

2. Яке явище називається гетероскедастичністю?

3. У чому полягає суть гетероскедастичності?

4. Яку форму звичайно має гетероскедастичність?

5. До яких наслідків призводить порушення припущення про гомоскедастичність?

6. Як встановити наявність гетероскедастичності?

7. Назвіть методи визначення гетероскедастичності.

8. За яких умов застосовується параметричний тест Гольдфельда -
Квандта?

9. У чому суть непараметричного тесту?

10. На чому базується тест Глейсера?

11. У чому суть трансформації моделі?

12. Наведіть форми гетероскедастичності в найпоширеніших випад­ках трансформації.

13. Які властивості мають оцінки параметрів трансформованої мо­делі?

14. За рахунок чого може існувати гетероскедастичність?

15. У чому суть узагальненого методу найменших квадратів?

Дата добавления: 2014-10-23