Алгоритм Фаррара–Глобера

Алгоритм Фаррара–Глобера застосовує три види статистичних критеріїв для виявлення мультиколінеарності:

• усього масиву незалежних змінних (критерій 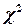(«хі-квадрат»));

• кожної незалежної змінної з усіма іншими (F - критерій);

• кожної пари незалежних змінних (t -критерій).

Порівнявши ці критерії з їх критичними значеннями, можна зро­бити конкретні висновки щодо наявності чи відсутності мультиколінеарності незалежних змінних.

Алгоритм Фаррара–Глобера складається з семи кроків.

1-й крок:

нормалізувати змінні 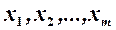економетричної моделі, обчисливши нові (нормалізовані) значення змінних

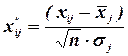(4.1),

де кількість спостережень (i = 1, 2,..., п); т – кількість незалежних 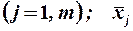– середня арифметична незалежної змінної 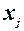; 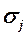– середнє квадратичне відхилення незалежної змінної .

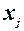2-й крок:

на основі матриці 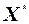, елементами якої є нормалізовані незалежні змінні 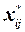, обчислити кореляційну матрицю (матрицю моментів нор­малізованої системи нормальних рівнянь):

(4.2)

де 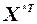– транспонована матриця 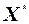(елементи матриці R характе­ризують щільність зв'язку однієї незалежної змінної з іншою);

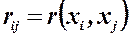– парні коефіцієнти кореляції.

3-й крок:

визначити 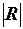- визначник кореляційної матриці R;

обчислити експериментальне значення критерію :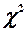

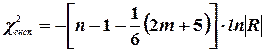(4.3),

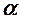порівняти значення з табличним при ступенях свободи і рівні значущості (якщо 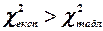, то в масиві незалежних змінних існує мультиколінеарність).

4-й крок:

визначити матрицю похибок:

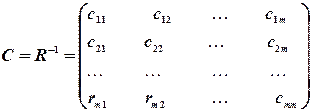(4.4).

5-й крок:

розрахувати F - критерії:

(4.5)

де діагональні елементи матриці С;

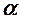експериментальні значення критеріїв порівняти з табличним при і ступенях свободи й рівні значущості (якщо 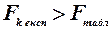, то відповідна незалежна змінна мультиколінеарна з іншими);

розрахувати коефіцієнти детермінації для кожної змінної:

(4.6).

6-й крок:

знайти часткові коефіцієнти кореляції, які характеризують щільність зв'язку між двома змінними за умови, що інші змінні не впливають на цей зв'язок (існування парної мультиколінеарності):

(4.7),

де 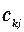- елементи матриці С.

Якщо порівняти конкретні числові значення часткових і парних коефіцієнтів, то можна побачити, що перші значно менші, ніж останні. Тому на основі знання парних коефіцієнтів кореляції висновок про мультиколінеарність робити неможливо. Для цього не­обхідно виконати 7-й крок.

7-й крок:

розрахувати t -критерії:

(4.8),

значення критеріїв 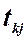порівняти з табличними при ступе­нях свободи та рівні значущості ; якщо , то між незалеж­ними змінними і 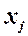існує мультиколінеарність.

Висновки:

1. Між незалежними змінними може існувати лінійна залежність, однак вона може й не бути явищем мультиколінеарності змінних, а тому не впливатиме на кількісні оцінки параметрів моделі, розра­хованих за допомогою звичайного МНК.

2. Якщ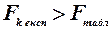о , то залежить від усіх інших незалежних змінних і треба вирішити питання про її виключення з переліку змінних.

3. Якщо , то і 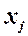щільно пов'язані між собою.

4. Аналізуючи F- і t - критерії, робимо висновок, яку зі змінних треба виключити з моделі (зрозуміло, якщоце можливо з економіко-логіко-теоретичних міркувань).

5. Якщо виконавши пп. 2-4, ми не досягли мети, тобто не усуну­ли мультиколінеарність, оцінку параметрів моделі слід обчислювати за допомогою іншого методу, наприклад методу головних компонентів (або однієї з його модифікацій).

Дата добавления: 2014-10-23