Природа автокореляції та її наслідки

ТЕМА 6. АВТОКОРЕЛЯЦІЯ

Розглянемо класичну лінійну багатофакторну модель

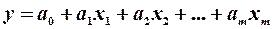(6.1),

або в матричному вигляді

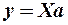(6.2),

де

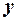– вектор-стовпець залежної змінної розмірності ;

– матриця незалежних змінних розмірності );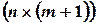

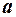– вектор-стовпець невідомих параметрів розмірності .

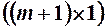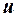– вектор-стовпець випадкових помилок розмірності .

.

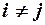Одним із припущень класичного регресійного аналізу є припу­щення про незалежність випадкових величин 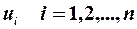.Якщо це припущення порушується (незважаючи на те, що дисперсія залишків є сталою – наявна гомоскедастичність), то ми маємо спра­ву з явищем, яке називається автокореляцією залишків.

Автокореляція залишків виникає найчастіше тоді, коли економетрична модель будується на основі часових рядів. Якщо існує кореля­ція між послідовними значеннями деякої незалежної змінної, то спо­стерігатиметься й кореляція послідовних значень залишків, так звані лагові затримки (запізнювання) в економічних процесах.

Автокореляція може виникати через інерційність і циклічність багатьох економічних процесів. Провокувати автокореляцію також може неправильно специфікована функціональна залежність у регресійних моделях.

Припустимо, модель (6.1) має автокорельовані залишки, тобто ви­падкові величини залежні між собою: .

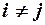Отже, як і у випадку гетероскедастичності, дисперсія залишків

. (6.3)

Але при гетероскедастичності змінюються дисперсії залишків за відсутності їх коваріації, а при автокореляції існує коваріація за­лишків за незмінної дисперсії.

Якщо проігнорувати наявність автокореляції залишків при оцінюванні параметрів моделі застосувати МНК, то можливі такі наслідки:

1. Оцінки параметрів моделі можуть бути незміщеними, але неефективними, тобто вибіркові дисперсії вектора оцінок 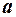можуть бути невиправдано великими.

2. Статистичні критерії статистик, які отримані для кла­сичної лінійної моделі, не можуть бути використані для дисперсій­ного аналізу, бо їх розрахунок не враховує наявності коваріації за­лишків.

3. Неефективність оцінок параметрів економетричної моделі, як
правило, призводить до неефективних прогнозів, тобто прогнозні зна­чення матимуть велику вибіркову дисперсію.

Висновки. За наявності автокореляції поширеним методом оціню­вання невідомих параметрів є узагальнений метод найменших квад­ратів, який було розглянуто в попередньому розділі. Отримані за допомогою УМНК оцінки є незміщеними та ефективними.

6.2. Тестування наявності автокореляції

Тестування наявності автокореляції, як правило, здійснюється за -тестом Дарбіна – Уотсона, хоча існують й інші не менш відомі тес­ти: критерій фон Неймана, нециклічний коефіцієнт автокореляції, циклічний коефіцієнт автокореляції.

6.2.1. Критерій Дарбіна – Уотсона

(складається з кількох етапів і включає зони невизначеності)

Крок 1. Розраховується значення -статистики за формулою

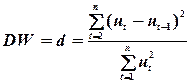. (6.4)

Зауваження. Доведено, що значення -статистики Дарбіна – Уот­сона перебуває в межах .

Крок 2. Задаємо рівень значущості . За таблицею значення -статистики Дарбіна –Уотсона при заданому рівні значущості , кількості факторів 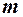і кількості спостережень 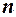знаходимо два значення 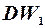і :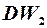

Якщо то наявна додатна автокореляція.

Якщо або ,ми не може­мо зробити висновки ані про наявність, ані про відсутність ав­токореляції (потрапляє в зону невизначеності).

Якщо маємо від'ємну автокореляцію.

Якщо то автокореляція відсутня.

Графічне зображення розподілу ілюструє рис. 6.1.

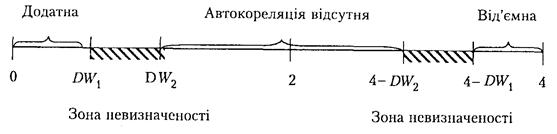
Рисунок 6.1 – Зони авто кореляційного зв’язку за критерієм Дарбіна –Уотсона

6.2.2. Критерій фон Неймана

За цим критерієм розраховується

Звідси 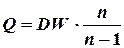. Отже, при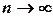

Фактичне значення критерію фон Неймана порівнюється з таб­личним при вибраному рівні значущості і заданій кількості спостережень : .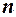

Якщо 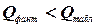, то автокореляція існує, у іншому випадку автокореляція відсутня.

6.2.3. Коефіцієнти автокореляції та їх застосування

Окрім статистик Дарбіна – Уотсона та Неймана, для перевірки ав­токореляції застосовують також нециклічний коефіцієнт автокореляції 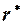, який відображає ступінь взаємозв’язку рядів і обчислюється формулою

Коефіцієнт 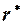може набувати значень в інтервалі . Його від'ємні значення свідчать про від'ємну автокореляцію залишків, а до­датні – про додатну автокореляцію. Значення, що лежать в деякій кри­тичній області поблизу нуля, підтверджують нульову гіпотезу про відсутність автокореляції в залишках. Оскільки імовірнісний розпо­діл 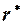встановити важко, то на практиці замість 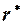обчислюють цик­лічний коефіцієнт автокореляції . Загалом, якщо часовий ряд має циклічний характер, тобто припускається, що після значення 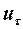загаль­ний характер зміни членів ряду повторюється, то автокореляцію виз­начають за допомогою коефіцієнта , запровадженого Андерсоном.

При цьому автокореляція визначається між послідовностями, зсу­нутими на період :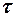

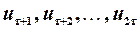
і

і

Якщо період 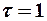, то маємо коефіцієнт циклічної автокореляції першого порядку, який відбиває інтенсивність взаємозв'язку між по­слідовностями

і

Для досить довгих рядів вплив циклічних членів стає незначним, тому імовірнісний розподіл коефіцієнта 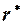наближається до імовір­нісного розподілу коефіцієнта циклічної автокореляції , який об­числюється за формулою

Якщо останній член ряду дорівнює першому, тобто , то нециклічний коефіцієнт автокореляції дорівнює циклічному. Очевид­но, якщо залишки не містять тренда, то припущення про рівність недалеке від дійсності й циклічний коефіцієнт автокореляції близький до нециклічного. Крім того, припускаючи, що середня за­лишків дорівнює нулю, тобто , а отже, ,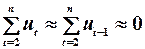

отримуємо приблизну формулу для обчислення циклічного коефіці­єнта автокореляції:

При цьому 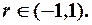Значення 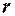використовується при оцінюванні параметрів моделі.

Дата добавления: 2014-10-23