Оцінювання параметрів дистрибутивно-лагових моделей

Для оцінювання параметрів дистрибутивно-лагових моделей зви­чайно застосовують два можливих підходи: послідовне оцінювання і апріорне оцінювання.

Ідея першого підходу полягає в тому, щоб поступово дослід­жувати вплив запізнених змінних на залежну змінну. Другий підхід базується па припущенні, що параметри моделі мають пев­ну закономірність, тобто пов'язані між собою деякими співвідно­шеннями.

Послідовне оцінювання параметрів виконується так: спочатку бу­дують регресію залежної та незалежної змінних в один і той самий момент часу, потім до моделі додають ще одну змінну — незалежну змінну в попередній момент часу, тобто розглядають залежність по­казника від двох змінних. Далі в регресію вводиться ще одна змінна — у момент часу, зсунутий на два попередніх проміжки, і т. д. Кожна з моделей досліджується па адекватність і значущість її параметрів. Процедура закінчується, коли параметри при лагових змінних почи­нають бути статистично незначущими та (або) коефіцієнт хоча б однієї змінної змінює свій знак.

Такий метод хоч і повний, однак має певні недоліки. По-перше, невідомою є максимальна тривалість лага, а це не дає змоги перед­бачити, скільки змінних увійде в модель. По-друге, між послідовними значеннями змінних здебільшого спостерігається висока кореляція, що породжує проблему мультиколінеарності в моделі. Крім того, через зменшення ступенів свободи в таких моделях оцінки стають дещо не­певними, що також знижує їх якість.

Наявність мультиколінеарності між лаговими змінними усклад­нює побудову моделі. Щоб усунути мультиколінеарність, на коефі­цієнти при лагових змінних накладають додаткові обмеження (апрі­орне оцінювання), а саме вибирають їх так, щоб вплив лага па досліджуваний показник був «односпрямований» (тобто коефіцієнти були б однакового знака) і зменшувався з кожним наступним кро­ком у минуле. Такі припущення реалізують, як правило, у моделях, де параметри змінюються в геометричній прогресії. Крім того, не­скінченна сума членів спадної геометричної прогресії є скінченою величиною, що дає змогу узагальнити модель з кінцевим лагом і зас­тосовувати однакові методи оцінювання параметрів.

Однак і в цьому разі залишається велика кількість оцінюваних па­раметрів.

Уведення в модель лагової залежної змінної (затримка на один період), відоме як перетворення Койка, значно спрощує модель:

(7.2).

Така модель містить не лише поточні, а й попередні значення за­лежної змінної, тобто є авторегресійною.

Заміна незалежних лагових змінних однією залежною змінною зменшує кількість оцінюваних параметрів і усуває проблему мультиколінеарності, однак призводить до нових труд­нощів. Наявність у моделі лагової залежної змінної потребує пере­вірки передумови про незалежність змінних і залишків при застосу­ванні звичайного МНК. Крім того, залишки моделі часто виявляються серійно корельованими, а тому при дослідженні їх на автокореляцію необхідно використати спеціальні тести.

Отримана алгебраїчним способом модель Койка позбавлена тео­ретичного обґрунтування і фактично є послідовною моделлю.

З певних економічних міркувань можна отримати моделі, що зовні нагадують модель Койка, але з іншою інтерпретацією коефіцієнтів лагових змінних. Такими моделями є модель адаптивних сподівань

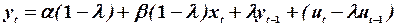(7.3)

та модель часткового коригування

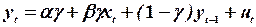(7.4)

Ці моделі відрізняються від моделі Койка наявністю вільного чле­на, але при цьому реалізують різні ідеї щодо економічної діяльності. У першій моделі відображено думку про те, що люди навчаються з попереднього досвіду, причому нещодавній досвід має більший вплив, аніж попередній; друга базується на тому, що через інертність економічної системи зміна одного економічного показника не одразу впливає на зміну іншого і відповідний рівень залежної змінної дося­гається через певний час.

7.3. Оцінювання параметрів авторегресійних моделей

Три авторегресійних моделі — Койка (7.2), адаптивних сподівань (7.3) і часткового коригування (7.4) — можна подати в загальній формі:

(7.5)

Наявність лагових залежних змінних у динамічних моделях ство­рює певні проблеми при оцінюванні параметрів: серед пояснюючих змінних є стохастичні (залежні лагові змінні), а також існує пробле­ма серійної кореляції залишків моделі та лагових змінних. Залежно від гіпотез щодо залишків таких моделей використовують відповідні методи оцінювання.

Гіпотеза 1. Залишки є нормально розподіленими випадковими ве­личинами з нульовим математичним сподіванням та сталою диспер­сією.

Гіпотеза 2. Залишки описуються авторегресійною схемою першо­го порядку:

.

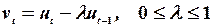Гіпотеза 3. Залишки автокорельоваиі та описуються авторегресій­ною схемою першого порядку:

,

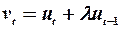крім того, .

Перша гіпотеза виконується лише для моделі часткового коригуван­ня (7.4); саме для неї можливе застосування звичайного МНК. Однак залежність залишків від лагової змінної у цій моделі призводить до зміщення оцінок параметрів. Та хоча оцінки параметрів будуть зави­щеними, вони матимуть найменшу середньоквадратичну похибку. І після визначення величини зміщення МНК-оцінки будуть найприйнятнішими.

Якщо залишки моделі визначаються через автокорельоваиі випад­кові величини, то МНК-оцінки параметрів моделі також матимуть зміщення, до того ж зміщення матиме також критерій Дарбіна—Уотсона. Тому для перевірки автокореляції залишків застосовують уза­гальнений критерій Дарбіна—Уотсона. Оцінювання параметрів та­ких моделей виконують узагальненим методом найменших квадратів (методом Ейткена), в операторі оцінювання якого

коригуючи матриця має вигляд:

.

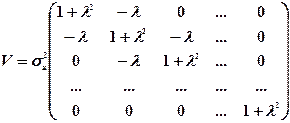Якщо лагову модель можна подати у вигляді:

,

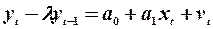то до перетворених у такий спосіб даних залежної змінної застосову­ють звичайний МНК. Причому параметр вибирають з інтервалу так, щоб мінімізувати суму квадратів залишків .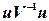

Якщо відносно залишків моделі приймається третя гіпотеза, то па­раметри оцінюють за допомогою таких методів:

1) класичного МНК після попереднього перетворення вхідних даних;

2) методу Ейткена (узагальненого МНК);

3) ітераційного методу;

4) методу інструментальних змінних;

5) алгоритму Уолліса.

Контрольні запитання

1. Що в економіці називається лагом?

2. Що є причиною лага?

3. Які регресійні моделі називають авторегресійними та дистрибутивно-лаговими?

4. Якою є природа авторегресійних моделей?

5. Які проблеми виникають при оцінюванні параметрів дистрибутивно-лагових і авторегресійних моделей?

6. Які гіпотези висуваються щодо залишків лагових моделей?

7. Якими методами оцінюються параметри дистрибутивно-лагових і авторегресійних моделей?

Дата добавления: 2014-10-23