Работа № 5. Итерационные циклы

Вычисляемые функции и массивы аргументов

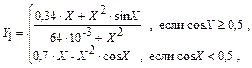где X = 4,5, -0,3, -1,5, -0,9, 0,2, 0,1, -1,8, 3,37, -4,5, 4,5.

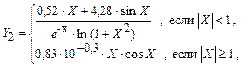где X = -2,5, -2,1, -0,78, 0,45, 0,65, 1,8, -0,18, -0,7, 4,8.

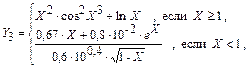где X = 0,44, -1,2, 2,5, 12,3, -1,65, 0,45, -3,3, -0,11, -0,45, -7,5.

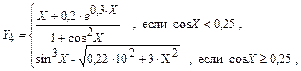где X = -8.3, -10,7, 7,25, 4,8, -5,1, 0,37, -1,5, 1,5, -1,5, 2,3, 0.4.

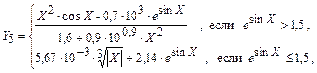где X = 0,01, 0,02, -0,5, 2,31, 0, 1,0, 0, -1,25, -1,0, -0,77, 0.

Рекомендации. При программировании вычисления функций Y следует анализировать возможность возникновения ошибок выполнения таких математических операций, как деление на ноль и вычисление логарифма нуля или отрицательного числа. Последняя ошибка может быть следствием неправомочного применения операции логарифмирования для вычисления целой степени произвольного числа (например, для вычисления cos²X).

Итерационным называется цикл, число повторений в котором заранее определить нельзя. Окончание такого цикла чаще всего происходит при дости­жении заданной точности расчета, а количество повторений зависит от вида вычисляемой функции, от выбора на­чального приближения и от точности вычислений.

Задание. Разработать блок-схемы и составить программы для решения нижеследующих задач.

1. Найти корень уравнения Х – 0,5× А ×sin(Х / А) + В = 0 методом последовательных приближений (методом итерации) с заданной степенью точности расчёта Е при начальном приближении Х ₀.

Пояснение. Чтобы воспользоваться методом итерации, необходимо исходное уравнение привести к виду Х _i+1 = F (Х _i). В простейшем случае это может быть сделано выражением одного из аргументов, например, так: Х _i+1 = 0,5× А ×sin(Х _i/ А) – В, где обозначения Х _i и Х _i+1 следует понимать как задаваемое (предыдущее) и расчётное (последующее) значения Х.

В идеальном случае Х = Х _i =X _i+1, что соответствует точному значению корня.

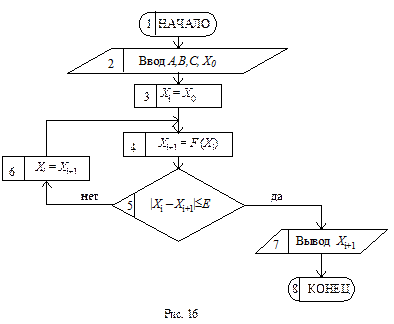
Блок-схема решения задачи приведена на рис. 16. Здесь в блоке №3 Х _i принимается равным заданному начальному значению Х₀ (подготовка цикла), а затем в теле цикла вычисляется значение Х _i+1. В блоке №5 производится проверка точности расчёта: если разница между предыдущим Х _i и последующим Х _i+1 значениями по модулю меньше или равна степени точности расчёта E, то цикл заканчивается; в противном случае Х _i получает новое значение в блоке №6 и цикл повторяется заново.

2. Найти сумму бесконечного ряда

Вычисление закончить, если очередное слагаемое по модулю окажется меньше заданной степени точности расчёта Е.

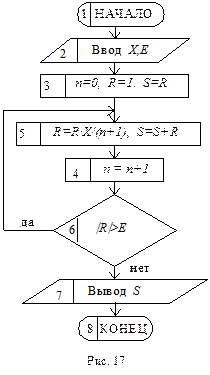Пояснение. При вычислении сумм рядов прежде всего необходимо иметь формулу для нахождения очередного члена ряда R. В данном примере каждый новый член ряда R _n+1 можно легко подсчитать по значению предыдущего R _n, а именно: R _n+1 = R _n× X/(n+1), где n – номер текущего члена ряда, n = 0,1,2, и т.д. При n =0 имеем начальное значение для первого члена ряда R =1, и начальное значение суммы ряда составляет этот единственный первый член ряда S = R.

Блок-схема решения приведена на рис. 17, причём в представляемом варианте различать R _n и R _n+1 нет необходимости, поэтому индексы у них опущены.

3. Организовать итерационный цикл для вычисления корня N -й степени

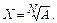
Расчёт вести по итерационной формуле Ньютона

с заданной степенью точности Е. В качестве начального приближения принять подкоренное выражение. Организовать подсчет количества итераций (количества повторений цикла).

4. Решить уравнение

2×А× Х – В× Х ² = 0,7× е ^{-2× Х}

относительно Х методом итерации с точностью до Е. Начальное приближение принять равным 0. Ввести ограничение на количество итераций: закончить вычисления при числе итераций больше 100. Вывести все последовательные приближения корня и порядковый номер итерации.

5. Для данного вещественного Х вычислить сумму Y ряда с заданной степенью точности (считать, что требуемая точность достигнута, если очередное слагаемое ряда по модулю меньше Е):

а)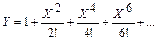

б)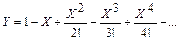

в) 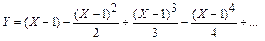(для 0<Х£2)

г)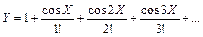

Контрольное задание № 5. Найти корень уравнения F (X) = 0 на интервале изоляции [ A,B ], воспользовавшись методом итерации. Работу выполнить в соответствии с представленными ниже пояснениями.

Таблица 5

№	Уравнение F (X) = 0	A	B
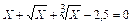
		0,4
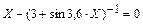
			0,5
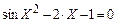
		-0,5
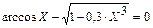
			0,9
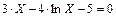
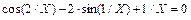
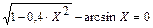
			0,9
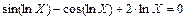
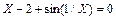
		1,2
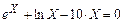
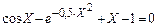
			1,5
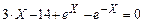
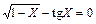
			0,9
		0,5
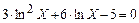
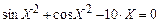
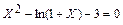
№	Уравнение F (X) = 0	A	B
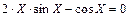
		0,4
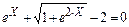
		-1	-0,2
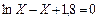
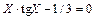
		0,2
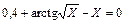
			0,9

Пояснения.

Дата добавления: 2014-10-23