Геометрический смысл определенного интеграла

Задача, приводящая к определенному интегралу.

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.

Пусть на [ a;b ] задана непрерывная неотрицательная функция y = f (x).

Определение 1. Криволинейной трапецией называется фигура, ограниченная осью абсцисс прямыми x = a, x = b и графиком функции y = f (x).

Ставится задача: вычислить площадь этой криволинейной трапеции (рис.13)

Рис.13

Решение.

1) Разобьем отрезок [ a;b ] на n частей точками x₀ = a; x₁; x₂; x_n-1; x_n = b и проведем прямые x = x₁, x = x₂, … x = x_т-1, которые разобьют трапецию на n частей.

2) Обозначим D x_k = x_k - x_k-1 – длины отрезков разбиения [ a;b ]. На каждом их отрезков произвольно выберем точку M_k (k = 1;… n).

Построим на каждом из отрезков прямоугольники с высотами, равными значению функции в выбранных точках M_k.

Площади полученных прямоугольников равны: S₁ = f (M₁) × D x₁; S₂ = f (M₂) × D x₂; ….; S_n = f (M_n) × D x_n.

3) Найдем сумму этих площадей:

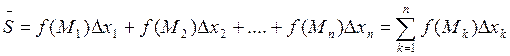
Получили площадь ступенчатой фигуры. Эта площадь зависит от способа разбиения отрезка [ a;b ] на части и от выбора на каждой из частей точек M_k (k = 1;… n).

Чем больше будет точек разбиения [ a;b ] на части и мельче по длине эти части, тем точнее сумма 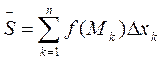будет приближаться к площади данной криволинейной трапеции. То есть можно записать:

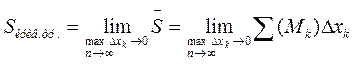
Определение 2. Сумма 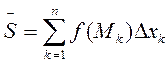называется интегральной суммой функции f (x) на отрезке [ a;b ].

Определение 3. Предел интегральной суммы S функции f (x) на [ a;b ] при n ® ¥ и max D x_k ® 0 называется определенным интегралом функции f (x) на отрезке [a;b], если этот предел существует и не зависит ни от способа разбиения [ a;b ] на части, ни от выбора точек M_k (k = 1;… n) на каждой из частей. Следовательно, можно записать:

.

При этом отрезок [ a;b ] называют отрезком интегрирования, “ a” –нижним пределом интегрирования, “b” –верхним пределом.

Теорема 1 (достаточное условие интегрируемости функции на [a;b])

Если функция f (x) на [ a;b ] непрерывна, то определенный интеграл 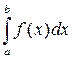существует, то есть функция f (x) на [ a;b ] интегрируема.

1)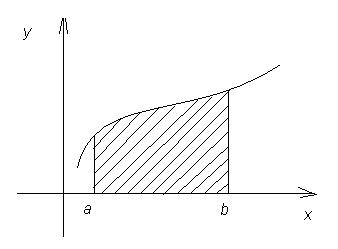

.

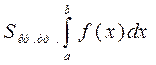2) Если область ограничена двумя кривыми y = f (x) и y = g (x), причем при xÎ [ a;b ] f (x) ³ g (x), то площадь области ограниченным кривыми y = f (x); y = g (x) и прямыми x = a, x = b вычисляется по формуле:

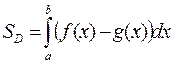
Дата добавления: 2014-10-15