Выбор математической модели пиролизной печи

Выбор математической модели для системы управления блоком пиролизных печей на крупнотоннажных установках производства этилена тесно связан с требованием практической реализации математической модели для оптимального управле­ния в реальном масштабе времени. При математическом описании процессов пиролиза бензина в трубчатых печах широко применяют два подхода: один осно­ван на изучении химизма и кинетики процесса, другой – на описании процесса с помощью формальных математических за­висимостей.

Кинетические модели. Системы автоматического регулирования пиролизной печи, в том числе и системы локальной оптимизации, используют для выработки управляющих воздействий на некоторые обобщенные характери­стики процесса (плотность сырья и пирогаза, температуру сме­си в реакционной зоне, жесткость пиролиза), не учитывая ки­нетики и химизма самого процесса.

Между тем процесс пиро­лиза характеризуется одновременным протеканием большого числа прямых и обратных реакций с различными группами углеводородов. В широком диапазоне технологических режимов изменение условий для протекания этих реакций может составлять значительные трудности при установлении оптимального режи­ма пиролизной печи. Кинетические же модели, учиты­вающие такие важные характеристики процесса, как углеводо­родный состав сырья и получаемого пирогаза, остаются адек­ватными в достаточно широком диапазоне изменения характери­стик объектов. Поэтому, основное распространение кинетические модели находят при выполнении расчетов технологического оборудования, а также при разработке технологического регламента для нового процесса.

Так, кинетическая модель, осно­ванная на схеме из основных семи превращений уг­леводородов при пиролизе, со­держит уравнения материального и теплового балансов, а так­же кинетические уравнения, устанавливающие зависимости ско­ростей химических реакций превращения углеводородов от внешних условий. Математическое описание модели записывается системой из 14-ти дифференциальных урав­нений элементарных балансов массы. Скорость реакции распада углеводородных групп при низких давлениях выражается уравнениями первого порядка.

Решение этой системы уравнений, описывающих ки­нетическую схему пиролиза, может быть выполнено на ЭВМ с использованием метода Рунге – Кутта с постоянным шагом интегрирования, однако точный расчет требует значи­тельных затрат времени и встречает ряд осложнений:

1) константы скоростей суммарных реакций носят обобщен­ный, условный характер для данного процесса и не имеют глу­бокого физического смысла, хотя при выбранной структуре ма­тематической модели могут адекватно описывать процесс в за­данной области изменения технологических режимов;

2) при необходимости проведения коррекции математиче­ской модели не всегда возможно определить, какие именно ко­эффициенты нуждаются в уточнении, что заставляет выпол­нять полный комплекс расчетов для всей математической мо­дели.

Для расчета пиролиза этана и пропана можно использовать кинетическую модель, базирующуюся на радикально-цеп­ной теории, согласно которой пиролиз рассматривается как цеп­ной процесс с участием свободных радикалов. Каждая ре­акция радикалов элементарна и по принципу независимости реакций остается неизменной при описании пиролиза различ­ных веществ. Однако такая кинетическая модель пиролиза включает 36 реакций и ее применение часто встречает значительные затруднения.

Смешанные модели. В наиболее общем виде кинетику процесса можно описать через разнообразные обобщенные показатели, вводимые в эмпирическую модель. Имея определенные свойства кинетических моделей, модели с обобщенными показателями удобны для реализации в системах управления реального времени. К таким показателям, напри­мер, относится комплексная характеристика жесткости крекин­га, определяемая по формуле

q = tt ^0,06, (7.12)

где q – параметр жесткости процесса; t – температура пирогаза на выходе из печи (°С); t – продолжительность пребывания сырья в реакционной зоне.

Одна из таких систем использует математическую мо­дель пиролиза бензина, записанную в следующем виде:

q_j = f_j (S_j, V_j, T_j, P_j); (7.13)

Y _{CH4, j} = f _{CH4, j} (lnq_j); (7.14)

Y_{n j} /Y _{CH4, j} = f_{n j} (lnq_j, P_{n j}), (7.15)

где S, V, Т, Р – параметры пиролизной печи (соответственно расходы сырья и пара, температура и давление пирогаза); Y _CH4 – содержание метана в пирогазе; j – номер печи в блоке; Y_n – содержание n -гo компонента в пиро­газе; P_{n j} – парциальное давление n -oгo компонента на выходе j -й печи; q – обобщенный кинетический показатель (жесткость крекинга). Парциальное давление компонентов для уравнения (7.15) вычисляют с учетом изменения объема, которое также выраже­но через функцию жесткости крекинга.

Математическую модель (7.13) – (7.15) применяют для на­хождения режимов пиролизных печей, обеспечивающих макси­мальный выход в любой текущий момент времени. Для реше­ния задачи оптимизации на ЭВМ пользуются методом крутого восхождения и методом центров.

Для жидкого углеводородного сырья жесткость крекинга определяют как натуральный логарифм отношения концентра­ций n -пентана в углеводородном сырье и в образующемся пи­рогазе:

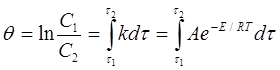, (7.16)

где С ₁, С ₂ – концентрации n -пентана соответственно в сырье и пирогазе; t – продолжительность пребывания сырья в реакционной зоне; А – предэкспоненциальный множитель; Е – энергия активации; R – универсальная газо­вая постоянная; Т – температура реакции.

С использованием кинетической функции жесткости (7.16) получены уравнения для определения выхода компонен­тов пирогаза:

G = g ₁ (a ₁ q + b ₁ q ²+ + c ₁ q ³ + d ₁ q ⁴) + g ₂ (a ₂ q + b ₁₂ q ²+ + c ₂ q ³ + d ₂ q ⁴) +

+ g ₃ (a ₃ q + b ₃ q ²+ + c ₃ q ³ + d ₃ q ⁴), (7.17)

где g ₁, g ₂, g ₃ – содержание в сырье соответственно n -парафиновых, изопара-финовых и парафиновых углеводородов. Это уравнение не учитывает содержание ароматических уг­леводородов, так как они в процессе пиролиза практически не дают газообразования и частично переходят во фракцию тяже­лого жидкого топлива.

Статистические модели. Статистические модели процесса пи­ролиза, полученные с использованием методов планирования эксперимента или по данным нормальной эксплуатации, обычно выражают в виде полиномов, содержащих в качестве аргумен­тов входные переменные процесса, которые нетрудно измерить датчиками, имеющимися на объекте. Выявление оптимальной структуры статистической модели (порядка уравнения, состава существенных факторов, значимых членов уравнений) часто осуществляют последовательным пе­ребором структур и их сопоставительным анализом, например, по коэффициенту множественной корреляции. При этом резуль­таты пассивного эксперимента обрабатывают с использованием стандартных программ корреляци­онно-регрессионного анализа.

Основной недостаток традиционного статистического метода перебора – неоднозначность и субъективность получаемой оп­тимальной структуры модели. Она зависит от квалифи­кации исследователя и ряда выбранных случайно показателей, таких, например, как первона­чальная структура модели, численные значения критериев оп­тимальности, начальный состав основных факторов и т. д. Кроме того, с увеличением числа факторов в модели и порядка уравнений резко возрастает число возможных вариан­тов структур, что затрудняет их сопоставление.

Несмотря на существенные различия технологических про­цессов, можно выделить и ранжировать группы параметров (факторов), последовательное введение которых в структуру модели (в соответствии с рангом) позволяет в значительной степени уменьшить неопределенность традиционного статисти­ческого метода перебора, а также сократить число рассчиты­ваемых на ЭВМ вариантов модели. Возможная ранжиров­ка параметров для основных технологических процессов нефтепере­работки и нефтехимии приведена в табл. 7.1.

Таблица 7.1.

Дата добавления: 2014-10-23