Корректировка коэффициентов адаптивной модели

Пиролизные печи подвержены воздействию неконтролируе­мых возмущений (отложение кокса на внутренних поверхно­стях пирозмеевиков, изменение состава сырья, старение техно­логического оборудования), что вызывает необходимость пе­риодической коррекции коэффициентов адаптивной модели. Ис­следования показывают, что такая коррекция может быть вы­полнена с использованием известных алгоритмов адаптации на базе текущей информации от объекта.

Итерационный метод. Пиролизная печь в общем случае может описыва­ться линейной математической моделью (без ограничения общности возмож­на и нелинейная модель объекта) вида

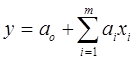, (7.31)

где у – выходной параметр; x_i – входные параметры (i =l, 2, …, m).

Тогда непрерывное уточнение оценок коэффициентов а модели (7.31) производится на каждом r -ом цикле формирования текущей информации от объекта с использованием алгоритма стохастической аппроксимации, запи­санном в дискретной форме как

, (7.32)

сходимость которого зависит от выбора последовательности

l ^(r) = f (N). (7.33)

В качестве последовательности, удовлетворяющей условиям сходимости данного алгоритма, часто используют зависимость вида

l ^(r) = 1/(A + BN^k). (7.34)

где N – конечное число итераций (или данных в экспериментальной выборке, r =1, 2,..., N); А, В, k – константы, обеспечивающие сходимость алгоритма с заданной скоростью.

Если наилучшие условия сходимости обеспечиваются при k = 0,5-1,0, то дать однозначные рекомендации по выбору констант А и В невозможно, так как они зависят еще и от при­нятой структуры математической модели (числа входных пере­менных, степени уравнения), а также способа формирования переменных и характеристик объекта управ­ления.

Следует отметить, что использование зависимости (7.34) для текущей коррекции коэффициентов математической модели сопряжено с необходимостью по истечении некоторого заданного числа шагов, начинать новую серию итераций. До получения новой модели (до шага N- 1) приходится пользоваться ранее полученной моделью, сформированной на (N-n)-ом цикле (n – номер цикла в текущий момент времени).

Поэтому при построении систем управления практическое применение получили стационарные алгоритмы адаптации, в которых коэффициент может быть постоянным или изменять­ся от входных переменных, но не зависит от числа итераций. При этом каждое новое поступающее от объекта измерение не­медленно используется для коррекции математической модели, и следовательно, модель «отстает» от объекта только на один цикл.

В стационарных алгоритмах в качестве последовательности l = f (x_i) часто используют зависимость вида

, (7.35)

где A и В – уточняемые константы.

Очевидно, что алгоритм адаптации с зависимостью (7.35) обладает большей динамичностью по сравнению с алгоритмом, в котором l= const, так как он позволяет регулировать («взве­шивать») процесс корректировки коэффициентов математиче­ской модели на каждом шаге в зависимости от значений пере­менных. Данная последовательность особенно эффективна, ес­ли все переменные, входящие в математическую модель, стан­дартизованы.

Экспериментальные исследования, проведенные с математи­ческой моделью вида (7.28), характеризующей содержание эти­леновой и пропиленовой фракций в пирогазе бензиновой печи, показали, что наилучшая сходимость стационарного алгоритма адаптации обеспечивается при выборе А = 0,1-1,0 и В = 0,0001-1,0.

Критерий оценки качества адаптации. При проведении ра­бот по моделированию с целью выбора типа и структуры мате­матической модели, варианта реализации системы управления или при оценке работы адаптационного алгоритма в процессе эксплуатации АСУ ТП необходимо иметь сопоставительную оценку, легко вычисляемую по имеющейся в системе текущей информации, поступившей от объекта управления.

Такую оценку можно выполнить сравнением среднеквадратических отклонений выходного параметра для вариантов S ₁, S ₂, …, S _m (k = 1, 2,..., m, где k – номер варианта, стадии или дискретного момента времени), вычисляемых по формуле

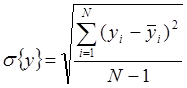, (7.36)

где y_i – значение выхода, полученное расчетом на математической модели (i = 1, 2,..., N); ` y_i – значение выхода, полученное прямым измерением на объекте, i – номер измерения.

Очевидно, что лучшим вариантом необходимо считать тот, для которого оценка s{ y } наименьшая.

При сопоставительной оценке вариантов реализации систем управления под выходными параметрами объекта управления можно рассматривать количественные па­раметры выпуска технологической продукции, их качественные характеристики, прогнозируемые по математической модели (работу системы управления в режиме «советчик оператору»), или управляющие воздействия (при работе системы в замкну­том контуре управления). Аналогичный характер имеют выход­ные параметры и при оценке адаптационных свойств матема­тической модели или качества работы алгоритма адаптации для эталонной модели системы.

Приложение А

Дата добавления: 2014-10-23