Теоретические модели объектов

Рассмотрим основные виды теоретических моделей линейных непрерывных стационарных динамических объектов и их взаимосвязь (действием шума e(t) пока пренебрегаем).

Дифференциальные уравнения. Наиболее универсальная модель, основанная на дифференциальных уравнениях, описывается выражением:

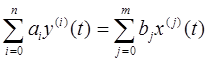, (Б.8)

где n — порядок модели (n > m); а_i и b_i — постоянные коэффициенты (параметры модели); x^(j)(t) и y⁽ⁱ⁾(t) — производные соответственно входного и выходного сигналов.

Уравнения переменных состояния. При выборе n координат системы x_i(t), i = 1, 2,..., n в качестве переменных состояния (такими координатами, например, могут быть выходной сигнал y(t) и n - 1 его производных) данную систему можно описать уравнениями для переменных состояния

Х '(t) = AX (t) + B u(t); (Б.9)

y(t) = СХ (t) + D u(t),

где X (t) = [ x ₁ (t), x ₂ (t), …, x _n (t) ]^T - вектор-столбец переменных состояния; В, С и D при скалярных u(t) и y(t) - соответственно матрица размера n ´ n, векторы размера n ´1 и 1´ n и скаляр (при векторных u(t) и y(t) - матрицы соответствующих размеров).

Применение преобразования Лапласа при нулевых начальных условиях к последним уравнениям позволяет получить следующее выражение для передаточной функции:

W(p) = C (p I - А) ^-1 В + D, (Б.10)

где I - единичная матрица. Отметим, что все приведенные модели являются эквивалентными, то есть, зная любую из них, можно получить все остальные.

Разностные уравнения. На практике в большинстве случаев измерение непрерывных сигналов производится в дискретные моменты времени t_k = kT (в данном случае Т — интервал дискретизации), что представляет определенное удобство при последующей обработке данных на ЭВМ. Для дискретных объектов наиболее общим видом описания является разностное уравнение (аналог дифференциального):

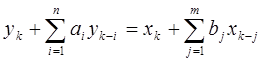, (Б.11)

где y_k-i = y [(k-i) T ] и x_k-j = x [(k-j) T ].

Z-преобразование. Связь сигналов может быть отражена также:

а) через дискретную свертку

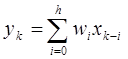, (Б.12)

где w_i — ординаты весовой решетчатой функции объекта;

б) с использованием аппарата Z -преобразования при z = e^pT:

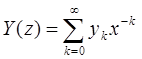; (Б.13)

в) через дискретную передаточную функцию:

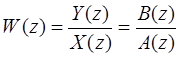, (Б.14)

которая определяется на основании разностного уравнения после применения к обеим его частям Z-преобразования:

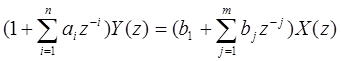. (Б.15)

Заметим, что Z -изображением решетчатой импульсной переходной характеристики является W(z), то есть Z { w_i } = W (z).

Непрерывные объекты можно приближенно отображать дискретными моделями. При этом возможны различные способы перехода от непрерывных моделей к дискретным:

а) с применением Z -преобразования со следующей цепочкой переходов:

W(p) ® L ^-1{ W (p)} = w (t) ® w (kT) = w_k ® W (z) = Z { w_k }; (Б.16)

б) заменой производных в дифференциальном уравнении, описывающем непрерывный объект, разностями вида

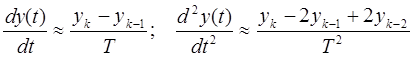и т. д. (Б.17)

(данный подход дает приемлемую точность только при малых Т);

в) с заменой 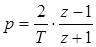(приближенный способ, предложенный А. Тастиным и называемый билинейным преобразованием), то есть

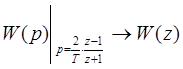. (Б.18)

Модели авторегрессии. Приведем ниже несколько распространенных моделей дискретных объектов для временной области, учитывающих действие шума наблюдения. Заметим, что множитель z ^-1= е ^-рТ представляет собой оператор задержки, то есть z ^-1 x_k = x_{k -l}, z ^-2 x_k = x_{k -2} и т. д. Моменты дискретного времени далее будем обозначать символом t, подразумевая, что в данном случае t = 0, 1, 2,...

Модель авторегрессии AR (AutoRegressive) считается самым простым описанием:

A (z) y (t) = e (t), (Б.19)

где A (z) = 1 + a ₁ z ^-1 + a ₂ z ^-2+...+ a_nz^-n.

ARX-модель (AutoRegressive with eXternal input) - более сложная:

A (z) y (t) = B (z) x (t) + e (t) (Б.20)

или в развернутом виде:

y (t) + a ₁ y (t -l) + a_ny (t-n) = b ₁ x (t) + b ₂ x (t -l)+...+ b_mx (t-m) + e (t).

Здесь и ниже e (t) — дискретный белый шум, В (z) = b ₁ + b ₂ z ^-l+...+ b _n z ^{- n+1}.

ARMAX-модель (Auto Regressive-Moving Average with eXternal input - модель авторегрессии скользящего среднего):

A (z) y (t) = B (z) x (t-nk) + C (z) e (t), (Б.21)

где nk - величина задержки (запаздывания), C (z)=1+ с ₁ z ^-1+ с ₂ z ^-2+…+ с _n z ^-n.

Модель «вход — выход» (в англоязычных источниках такая модель называется «Output-Error», то есть «выход — ошибка», сокращенно ОЕ):

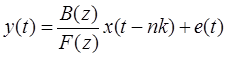, (Б.22)

где F (z)=1+ f ₁ z ^-1+ f ₂ z ^-2+…+ f_nf z ^{- nf}.

Модель Бокса — Дженкинса (BJ):

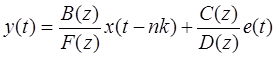, (Б.23)

(полиномы B (z), F (z), C (z) определены ранее, a F (z)=1+ d ₁ z ^-1+ d ₂ z ^-2+…+ d_nd z ^{- nd}).

Данные модели можно рассматривать как частные случаи обобщенной параметрической линейной структуры

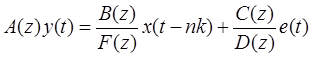, (Б.24)

при этом все они допускают расширение для многомерных объектов, имеющих несколько входов и выходов.

Модель для переменных состояния (State space):

х(t+ 1 ) = A x(t) + B u(t); (Б.25)

y(t) = С х(t) + D u(t)+v(t),

где А, B, C, D — матрицы соответствующих размеров, v (t) - коррелированный шум наблюдений.

Возможна и другая (так называемая обновленная или каноническая) форма представления данной модели:

x (t + 1) = A x (t) + B u (t) + K e (t); (Б.26)

y (t) = C x (t) + D u (t) + e (t),

где К - некоторая матрица (вектор-столбец), e (t) - дискретный белый шум (скаляр).

Приложение В

Дата добавления: 2014-10-23