Задачи оптимизации

ЗАДАЧИ И МЕТОДЫ ОПТИМИЗАЦИИ

Общая формулировка задачи параметрической оптимизации сводится к нахождению набора параметров х = (х₁, х₂, …, х_n), который является оптимальным в смысле некоторого критерия. В простейшем случае такая задача сводится к минимизации или максимизации некоторой (целевой) функции без каких-либо ограничений. В более сложных ситуациях на отмеченные параметры могут быть наложены некоторые ограничения в виде равенств, неравенств и параметрических границ. Краткий перечень возможных оптимизационных задач приведен в табл. В.1.

Таблица В.1.

№	Тип задачи	Математическая запись
	Скалярная минимизация	min f (a), a1< a< a 2
	Безусловная минимизация	min f (x)
	Линейное программирование	min f ^Tx, при условиях A×x £ b, Aeq×x = beq , xL£ x £ xU
	Квадратичное программирование	min ½ xHx+ f ^Tx, при условиях A×x £ b, Aeq×x = beq , xL£ x £ xU
	Минимизация при наличии ограничений	min f (x), при условиях с(x) £ 0, сeq(x) = 0 A×x £ b, Aeq×x = beq ,xL£ x £ xU
	Достижение цели	min g, при условиях F(x) - wg = g, с(x) £ 0, сeq(x) = 0 A×x £ b, Aeq×x = beq , xL£ x £ xU
	Минимакс	min max {Fi (x)}, при условиях с(x) £ 0, сeq(x) = 0 A×x £ b, Aeq×x = beq , xL£ x £ xU
	Полубесконечная минимизация	min f (x), при условиях K(x,w) £ 0 для всех w, с(x) £ 0, сeq(x) = 0 A×x £ b, Aeq×x = beq , xL£ x £ xU

Принятые обозначения: а - скалярный аргумент; х, g - векторный аргумент;

f (a), f (х) - скалярные функции; F (x), с (x), с_eq (x), K (x, w) - векторные функ-ции; A, A _eq, H - матрицы; b, b _eq, w, g - векторы; x _L, x _U - соответственно нижняя и верхняя граница области изменения аргумента.

Формулировка задачи параметрической оптимизации представляется следующим образом:

требуется найти вектор х, обеспечивающий

min f (x) при ограничениях

g_i(x) = 0 (i = 1, 2, …, m_e); (В.1)

g_i(x) £ 0 (i = m_e+1, …, m);

x _L£ x £ x _U,

где х - вектор оптимизируемых параметров (х Î Rⁿ); f(x) - скалярная целевая функция (критерий) векторного аргумента (f(x): Rⁿ ® R); g_i(x) - также некоторые скалярные функции векторного аргумента. Заметим, что задача максимизации сводится к задаче минимизации заменой f(x) на -f(x).

Эффективность и точность решения данной задачи зависит как от числа параметров и ограничений, так и от вида целевой функции. При линейных ограничениях и целевой функции приведенная задача называется задачей линейного программирования, при линейных ограничениях, но при квадратичной (по аргументу) целевой функции - задачей квадратичного программирования, в общем случае - это задача нелинейного программирования.

Безусловная оптимизация. Существующие алгоритмы безусловной оптимизации могут быть разделены на две группы: алгоритмы, базирующиеся на использовании производных минимизируемой функции (градиентные и методы второго порядка), и алгоритмы, использующие только значения функции (безградиентные).

Безградиентные методы (например, симплексный метод Нелдера-Мида) более пригодны для задач, где минимизируемая функция является существенно нелинейной или имеет разрывы.

Градиентные методы используют информацию о наклоне функции для выбора направления поиска экстремума. Градиентные методы первого порядка обычно эффективны в случаях целевых функций, непрерывных вместе с первыми производными. В одном из таких методов - наискорейшего спуска, на каждой итерации движение к точке минимума осуществляется в направлении - Ñf(x) (где Ñf(х) - вектор-градиент целевой функции f(x)).

Однако этот метод весьма неэффективен если поверхность целевой функции имеет узкие «овраги», например, как у известной функции Розенброка (поверхность этой функции приведена на рис. В.1)

Рис. В.1. Графическое представление функции Розенброка f(x)= 100(x ₁ -x ₂²)²+(1- x ₁)²

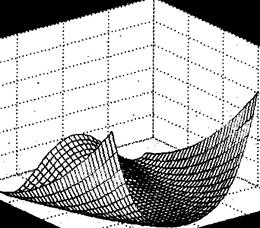
Минимальное значение данной функции, как нетрудно видеть, равно нулю при x ₁ = х ₂ = 1. Между тем численные эксперименты показывают, что зачастую метод наискорейшего спуска не обеспечивает нахождение точки экстремума даже после сотен и тысяч итераций. Отметим, что указанную функцию из-за своеобразной формы ее линий равного уровня часто называют "банановой" функцией и используют как тестовую при проверке эффективности различных оптимизационных алгоритмов.

Квазиньютоновские алгоритмы являются наиболее распространенными среди алгоритмов, использующих информацию о градиенте. В этих итерационных алгоритмах целевая функция в окрестностях произвольной точки аппроксимируется квадратичной функцией, при этом на каждой итерации решается задача локальной минимизации:

min ½ x ^T Hx + c ^T x + b, (В.2)

где Н - симметричная и положительно определенная матрица вторых частных и смешанных производных (матрица Гессе или гессиан), с – постоянный вектор, b - кон­станта.

Оптимальное решение приведенной задачи соответствует нулевым значениям первых производных, т.е.

Ñf (x *) = Hx * + c = 0, (В.3)

отсюда

x * = - H ^-1 c.

Среди подобных алгоритмов одним из наиболее популярных и используемых в пакете Optimization является так называемый BFGS-алгоритм, получивший свое на­звание по фамилиям предложивших его авторов (Broyden, Fletcher, Goldfarb, Shanno). Здесь аппроксимация Н производится итерационно. Рассчитывая на очередной итерации новое направление, он осуществляет движение до достижения минимума целевой функции с использова­нием методов одномерного поиска.

Алгоритмы Ньютона-Гаусса и Левенберга-Марквардта являются методами второго порядка и применяются реже, поскольку требуют больших вычислительных затрат для расчета матриц вторых производных. Они используются в основном для решения задачи нелинейного метода наименьших квадратов (МНК).

Минимизация при наличии ограничений. В задачах оптимизации с ограничениями (см. табл. В.1) обычный подход в нахождении решения состоит в замене исходной задачи на задачу без ограничений (задачу безусловной оптимизации), например с помощью метода штрафных функций.

В настоящее время, однако, более эффективным считается применение так называемых уравнений Куна-Таккера, которые на основании вышеприведенной формулировки задачи параметрической оптимизации и при некоторых дополнительных предположениях о характере ограничений записываются в виде:

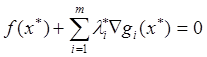; (В.4)

, i= 1, 2, …, m_e;

l _i^*= 0, i= m_e +1, …, m,

где l _i - множители Лагранжа.

Для решения данных уравнений в пакете Optimization использован алгоритм так называемого последовательного квадратичного программирования (в оригинале Se­quential Quadratic Programming или SQP), представляющий собой по сути разновид­ность квазиньютоновского метода. Основная идея SQP заключается в применении квадратичной аппроксимации для учитывающей ограничения функции Лагранжа

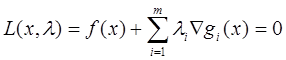. (В.5)

В последней формулировке данная задача может быть решена любым методом решения задач квадратичного программирования. В пакете Optimization для этой цели использован комбинированный алгоритм, объединяющий алгоритм BFGS и так назы­ваемый метод проекций.

Многокритериальная оптимизация. Достаточно часто в реальных ситуациях качество работы исследуемого объекта или системы оценивается не единственным критерием или показателем качества, а совокупностью таких критериев, причем представляющихся одинаково значимыми. Это приводит к задаче оптимизации с векторной целевой функцией F(x) = {F₁(x), F₂(x),..., F_k(x)} и формулировкой

min F (x) при ограничениях

g_i(x) = 0 (i = 1, 2, …, m_e); (В.6)

g_i(x) £ 0 (i = m_e+1, …, m);

x _L£ x £ x _U,

получившей название задачи многокритериальной или векторной оптимизации.

Известно, что решение подобной задачи сводится к нахождению множества точек неулучшаемых решений (Парето-множества), для чего используется, на­пример, метод взвешенной суммы частных критериев или метод e-огра­ничений.

В рассматриваемом пакете для решения задачи многокритериальной оптимизации применен так называемый метод достижения цели, предложенный Gembicki и мате­матически описывающийся соотношениями

min g, при ограничениях

F _i (x) - w _i g £ F _i^*, i= 1, 2, …, m,(В.7)

где Q - область допустимых значений х; w _i - некоторые весовые коэффициенты; F _i^* - некоторые устанавливаемые "цели" (goals).

В приведенной формулировке задача подобна задаче однокритериальной оптими­зации и может решаться с помощью выше отмеченных алгоритмов.

Алгоритмы большой размерности. Задачи оптимизации с большим числом оптимизируемых факторов (десятки, сот­ни, тысячи) и/или сложным, нелинейным характером целевой функции достаточно плохо решаются рассмотренными методами ввиду существенных вычислительных затрат (например, при определении аппроксимации матрицы Гессе), что привело к выделению в отдельную группу алгоритмов большой размерности, оказывающихся эффективными в подоб­ных ситуациях.

Данные алгоритмы основаны на идее так называемой области доверия - области N вблизи некоторой точки х, в которой рассматриваемая целевая функция f(x) может быть адекватно аппроксимирована более простой функцией q(s), так что исходная за­дача оптимизации сводится к задаче

min q (s), s ÎN. (В.8)

Текущая точка х обновляется, т.е. заменяется точкой x + s, если f(x + s) < f(x), и не из­меняется - в противоположном случае. В стандартном подходе предполагается, что как функция q(s), так и область дове­рия описываются квадратичными функциями.

Приложение Г

Дата добавления: 2014-10-23