Дисперсия

Для того, чтобы иметь представление о поведении случайной величины, недостаточно знать только ее математическое ожидание. Рассмотрим две случайные величины: Х и Y, заданные рядами распределения вида

Х
р	0,1	0,8	0,1

Y
p	0,5	0,5

Найдем М (Х) = 49·0,1 + 50·0,8 + 51·0,1 = 50, М (Y) = 0·0,5 + 100·0,5 = 50. Как видно, мате-матические ожидания обеих величин равны, но если для Х М (Х) хорошо описывает пове-дение случайной величины, являясь ее наиболее вероятным возможным значением (при-чем остальные значения ненамного отличаются от 50), то значения Y существенно отсто-ят от М (Y). Следовательно, наряду с математическим ожиданием желательно знать, на-сколько значения случайной величины отклоняются от него. Для характеристики этого показателя служит дисперсия.

Определение. Дисперсией (рассеянием) случайной величины называется математи-ческое ожидание квадрата ее отклонения от ее математического ожидания:

D (X) = M (X – M (X))².

Пример. Найдем дисперсию случайной величины Х (числа стандартных деталей среди отобранных) в примере 1 данной лекции. Вычислим значения квадрата отклонения каждого возможно-го значения от математического ожидания:

(1 – 2,4)² = 1,96; (2 – 2,4)² = 0,16; (3 – 2,4)² = 0,36. Следовательно,

Замечание 1. В определении дисперсии оценивается не само отклонение от среднего, а его квадрат. Это сделано для того, чтобы отклонения разных знаков не компенсировали друг друга.

Замечание 2. Из определения дисперсии следует, что эта величина принимает только неотрицательные значения.

Замечание 3. Существует более удобная для расчетов формула для вычисления дисперсии, справедливость которой доказывается в следующей теореме:

Теорема. D (X) = M (X ²) – M ²(X).

Доказательство.

Используя то, что М (Х) – постоянная величина, и свойства математического ожидания, преобразуем формулу (7.6) к виду:

D (X) = M (X – M (X))² = M (X ² - 2 X·M (X) + M ²(X)) = M (X ²) – 2 M (X)· M (X) + M ²(X) =

= M (X ²) – 2 M ²(X) + M ²(X) = M (X ²) – M ²(X), что и требовалось доказать.

Пример. Вычислим дисперсии случайных величин Х и Y, рассмотренных в начале этого раздела. М (Х) = (49²·0,1 + 50²·0,8 + 51²·0,1) – 50² = 2500,2 – 2500 = 0,2.

М (Y) = (0²·0,5 + 100²·0,5) – 50² = 5000 – 2500 = 2500. Итак, дисперсия второй случайной величины в несколько тысяч раз больше дисперсии первой. Таким образом, даже не зная законов распределения этих величин, по известным значениям дисперсии мы можем утверждать, что Х мало отклоняется от своего математического ожидания, в то время как для Y это отклонение весьма существенно.

Свойства дисперсии.

1) Дисперсия постоянной величины С равна нулю:

D (C) = 0.

Доказательство. D (C) = M ((C – M (C))²) = M ((C – C)²) = M (0) = 0.

2) Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:

D (CX) = C ² D (X). Доказательство. D (CX) = M ((CX – M (CX))²) = M ((CX – CM (X))²) = M (C ²(X – M (X))²) =

= C ² D (X).

3) Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:

D (X + Y) = D (X) + D (Y). (7.10)

Доказательство. D (X + Y) = M (X ² + 2 XY + Y ²) – (M (X) + M (Y))² = M (X ²) + 2 M (X) M (Y) +

+ M (Y ²) – M ²(X) – 2 M (X) M (Y) – M ²(Y) = (M (X ²) – M ²(X)) + (M (Y ²) – M ²(Y)) = D (X) + D (Y).

Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме их дисперсий.

Следствие 2. Дисперсия суммы постоянной и случайной величин равна дисперсии случайной величины.

4) Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:

D (X – Y) = D (X) + D (Y). Доказательство. D (X – Y) = D (X) + D (- Y) = D (X) + (-1)² D (Y) = D (X) + D (X).

Дисперсия дает среднее значение квадрата отклонения случайной величины от среднего; для оценки самого отклонения служит величина, называемая средним квадратическим отклонением.

Определение. Средним квадратическим отклонением σ случайной величины Х называется квадратный корень из дисперсии:

.

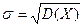Пример. В предыдущем примере средние квадратические отклонения Х и Y равны соответственно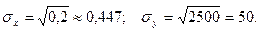

Дата добавления: 2014-10-23