Случайные величины. Понятие случайной величины

Понятие случайной величины. Дискретные и непрерывные

Тема 16. Случайные величины и способы их описания

Виды случайных величин. Задание дискретной случайной величины. Числовые характеристики дискретных случайных величин. Закон больших чисел и его следствие. Неравенство Чебышева. Функция распределения вероятностей случайной величины. Плотность распределения вероятностей непрерывной случайной величины. Нормальное распределение. Показательное распределение.

Случайная величина является одним из основных понятий теории вероятностей.

Под случайной величиной понимается переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно – заранее неизвестно).

Примеры случайных величин:

1) число появлений «орла» при последовательном бросании монеты несколько раз;

2) количество бракованных изделий в данной партии;

3) урожай с одной сотки;

4) интервал времени между двумя последовательными появлениями автобуса на данной остановке;

5) дальность полета артиллерийского снаряда;

6) расход электроэнергии на предприятии за месяц.

Случайные величины будем обозначать заглавными буквами латинского

алфавита Х, У, Z, …, а их значения – соответствующими строчными буквами х,у,z,….

В зависимости от характера области возможных значений можно выделить два вида случайных величин: дискретные и непрерывные.

Случайная величина называется дискретной, если она принимает лишь отдельные изолированные значения, которые можно перечислить (прим. 1-3).

Непрерывной называют величину, которая может принимать все значения из некоторого конечного или бесконечного интервала числовой оси (примеры 4-6).

Случайная величина обладает характерной особенностью. Мы можем указать область ее возможных значений, но не можем заранее знать, какое конкретное значение примет эта величина, т.к. оно меняется от испытания к испытанию.

Для изучения случайной величины необходимо указать не только область ее возможных значений, но и то, как часто принимается этой величиной определенное значение, т.е. вероятность этих значений.

Соответствие между областью возможных значений случайной величины и множеством вероятностей этих значений носит название закона распределения случайной величины.

Закон распределения является наиболее полным, исчерпывающим описанием случайной величины. Закон распределения вероятностей дискретной случайной величины.

Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически.

При табличном задании закона распределения дискретной случайной величины первая строка содержит все возможные значения случайной величины, перечисленные в порядке возрастания, а вторая – их вероятности:

Х	х1	х2	…	хi	…	хп
р	р1	р2	…	рi	…	рп

Такая таблица называется рядом распределения дискретной случайной величины.

События 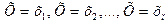образуют полную группу, следовательно сумма их вероятностей равна 1:

Ряд распределения для наглядности может быть изображен графически, если в прямоугольной системе координат построить точки 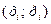, а затем соединить их отрезками. Полученную фигуру называют многоугольником или полигоном распределения вероятностей (рис. 2)

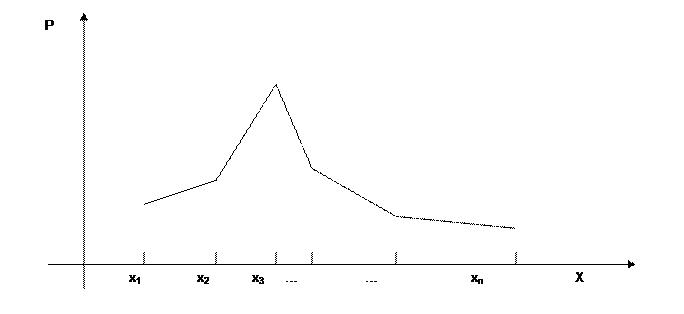
Рис.2

Такое описание случайной величины Х неприменимо для непрерывной случайной величины, т.к., во-первых, нельзя перечислить все бесконечное несчетное множество ее значений; во-вторых, вероятности каждого отдельно взятого значения непрерывной случайной величины равны нулю.

Дата добавления: 2014-10-23