
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Локальная теорема Муавра- Лапласа
|
|
|
|
При больших значениях п пользоваться формулой Бернулли достаточно трудно, т.к. формула требует выполнения действий над громадными числами.
Вычислить интересующую нас вероятность можно и, не прибегая к формуле Бернулли. Локальная теорема Муавра-Лапласа дает асимптотическую формулу, позволяющую приближенно найти вероятность появления события ровно k раз в п испытаниях, если число испытаний достаточно велико (функцию  (x) называют асимптотическим приближением функции f(x), если lim
(x) называют асимптотическим приближением функции f(x), если lim = 1).
= 1).
Теорема.Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность
Рп(k) 
 (16),
(16),
где  (x)=
(x)=
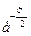 - функция Гаусса и х=
- функция Гаусса и х= .
.
Для упрощения расчетов, связанных с применением формулы (16), составлена таблица значений функции  . Пользуясь этой таблицей, необходимо иметь в виду свойства функции
. Пользуясь этой таблицей, необходимо иметь в виду свойства функции  (x):
(x):
Функция  (x) является четной, т.е.
(x) является четной, т.е.  (-x)=
(-x)=  ;
;
Функция  (x) – монотонно убывающая при положительных значениях х, причем при
(x) – монотонно убывающая при положительных значениях х, причем при 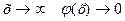 . (Практически можно считать, что уже при
. (Практически можно считать, что уже при 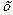 >4
>4  ).
).
Пример. В некоторой местности из каждых 100 семей 80 имеют автомобили. Найти вероятность того, что из 400 семей 300 имеют автомобили.
Решение. Вероятность того, что семья имеет автомобиль, равна 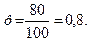 Т.к. п =100 достаточно велико, применяем локальную теорему Муавра-Лапласа. Найдем х:
Т.к. п =100 достаточно велико, применяем локальную теорему Муавра-Лапласа. Найдем х:

Интегральная теорема Муавра-Лапласа
Пусть в условиях примера 7.5.4 необходимо найти вероятность того, что от 300 до 360 семей (включительно) имеют автомобили. По теореме сложения вероятность искомого события

Каждое слагаемое можно вычислить по теореме Муавра-Лапласа, но большое количество слагаемых делает расчет весьма громоздким. В таких случаях используется следующая теорема.
15.7. Интегральная теорема Муавра-Лапласа.
Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Рп(k1,k2) того, что событие А появится в п испытаниях от k1 до k2 раз (включительно), приближенно равна
 (22),
(22),
где  и
и  или
или
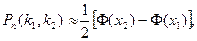 где
где  - функция Лапласа,
- функция Лапласа,
 .
.
Чем больше п, тем точнее эта формула. При выполнении условия npq>20 формула (16), так же, как и локальная, дает удовлетворительную для практики погрешность вычислений.
Функция  табулирована. Для применения этой таблицы нужно знать
табулирована. Для применения этой таблицы нужно знать
Свойства функции :
:
Функция  нечетная, т.е.
нечетная, т.е. 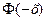 = -
= - 
Функция  монотонно возрастающая, причем при
монотонно возрастающая, причем при 

Пример. По данным примера 7.5.4. вычислить вероятность того, что от 300 до 360 (включительно) семей из 400 имеют автомобили.
Решение. npq =  . Применим интегральную теорему Муавра-Лапласа.
. Применим интегральную теорему Муавра-Лапласа.

Контрольные вопросы и задания для самостоятельной подготовки:
1. Теорема сложения вероятностей несовместных событий.
2. Полная группа событий.
3. Противоположные события.
4. Произведение событий. Условная вероятность.
5. Теорема умножения вероятностей.
6. Независимые события. Теорема умножения для независимых событий.
7. Вероятность появления хотя бы одного события.
8. Теорема сложения вероятностей совместных событий.
9. Формула полной вероятности.
10. Вероятность гипотез. Формула Байеса.
11. Формула Бернулли.
12. Локальная теорема Лапласа.
13. Интегральная теорема Лапласа.
14. Вероятность попадания в цель для первого стрелка равна 0,8, для второго – 0,7, для третьего – 0,9. Какова вероятность того, что в мишени 3 пробоины?
15. Из группы студентов 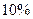 знают английский язык, 5%-французский и 1% - оба языка. Какова вероятность того, что наугад выбранный студент не знает ни одного иностранного языка?
знают английский язык, 5%-французский и 1% - оба языка. Какова вероятность того, что наугад выбранный студент не знает ни одного иностранного языка?
16. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором 3 вопроса.
17. Вероятность попадания стрелка в мишень при каждом выстреле равна0,8. Найти вероятность того, что после двух выстрелов мишень окажется поврежденной.
18. На 100 лотерейных билетов приходится 5 выигрышных. Какова вероятность выигрыша хотя бы по одному билету, если приобретено 4 билета.
19. Вероятность попадания стрелка в мишень при одном выстреле равна 0,2. Сколько выстрелов должен сделать стрелок, чтобы с вероятностью не менее 0,9 попасть в цель хотя бы один раз?
20. Вероятность того, что студент сдаст первый экзамен, равна 0,9, второй – 0,9, третий – 0,8. Найти вероятность того, что студентом будут сданы по крайней мере 2 экзамена.
21. Причиной разрыва электрической цепи служит выход из строя элемента  или одновременный выход из строя двух элементов -
или одновременный выход из строя двух элементов -  и
и 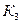 . Элементы могут выйти из строя независимо друг от друга с вероятностями, равными соответственно 0,1, 0,2, 0,3. Какова вероятность разрыва электрической цепи?
. Элементы могут выйти из строя независимо друг от друга с вероятностями, равными соответственно 0,1, 0,2, 0,3. Какова вероятность разрыва электрической цепи?
22. В магазин поступила новая продукция с трех предприятий в процентном составе: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия. Известно, что 10% продукции первого предприятия высшего сорта, второго предприятия - 5%, третьего предприятия - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная нами продукция окажется высшего сорта.
23. Два стрелка независимо друг от друга стреляют по мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень первого стрелка равна 0,8; для второго стрелка – 0,4. После стрельбы в мишени обнаружена одна пробоина. Какова вероятность того, что она принадлежит второму стрелку?
24. Сколько раз надобросить монету, чтобы с вероятностью 0,6 можно было ожидать, что отклонение относительной частоты появлений герба от вероятности р= 0,5 окажется по абсолютной величине не более 0,01?
|
|
|
|
|
Дата добавления: 2014-10-23; Просмотров: 2121; Нарушение авторских прав?; Мы поможем в написании вашей работы!