
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула Бернулли
|
|
|
|
Повторные независимые испытания
Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.
Если независимые повторные испытания проводятся при одном и том же комплексе условий, то вероятность наступления события А в каждом испытании одна и та же.
Описанная последовательность независимых испытаний получила название схемы Бернулли.
Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Условимся, что вероятность события А в каждом испытании равна р. Следовательно, вероятность ненаступления события А также постоянна и равна q=1-p.
Вычислим вероятность того, что в п испытаниях событие А осуществится ровно k раз и, следовательно, не осуществится 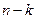 раз. Важно подчеркнуть, что не требуется, чтобы событие А повторялось ровно k раз в определенной последовательности. Например, если речь идет о появлении события А два раза в трех испытаниях
раз. Важно подчеркнуть, что не требуется, чтобы событие А повторялось ровно k раз в определенной последовательности. Например, если речь идет о появлении события А два раза в трех испытаниях 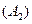 , то возможны следующие сложные события:
, то возможны следующие сложные события:
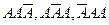 , т.е.
, т.е. 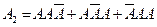 .
.
Вероятность одного сложного события, состоящего в том, что в п испытаниях событие А наступит k раз и не наступит 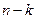 раз, по теореме умножения вероятностей для независимых событий равна
раз, по теореме умножения вероятностей для независимых событий равна 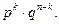 Таких сложных событий столько, сколько можно составить сочетаний из п элементов по k элементов, т.е.
Таких сложных событий столько, сколько можно составить сочетаний из п элементов по k элементов, т.е. 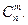 Так как эти сложные события
Так как эти сложные события  несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий, т.е. вероятности одного сложного события, умноженной на их число:
несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий, т.е. вероятности одного сложного события, умноженной на их число:
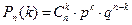 (13) - формула Бернулли.
(13) - формула Бернулли.
Пример. Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найти вероятности возможного числа появления бракованных деталей среди 5 отобранных.
Решение. Вероятность изготовления бракованной детали р = 1-0,8 =0,2. Искомые вероятности находим по формуле Бернулли:

Полученные вероятности изобразим графически точками с координатами (k,Рп(k)). Соединяя эти точки, получим многоугольник или полигон распределения вероятностей (Рис.1).

Рис.1
Рассматривая многоугольник распределения вероятностей, мы видим, что есть такие значения k (в данном случае k0=1), обладающие наибольшей вероятностью. Число k0 наступления события А в п независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события Рп(k0) по крайней мере не меньше вероятностей других событий Рп(k) при любом k. Для нахождения k0 используют неравенство
np-q k0
k0 np+q (14),
np+q (14),
полученное при решении системы неравенств:
Рп(k0) Рп(k0+1),
Рп(k0+1),
Рп(k0) Рп(k0-1). (15)
Рп(k0-1). (15)
Пример. Найдем наивероятнейшее число появления бракованных деталей из 5 отобранных и вероятность этого числа по данным примера
Решение. По формуле (15)
5 0,2 – 0,8 k0
k0  5 0,2 + 0,2
5 0,2 + 0,2
0,2  k0
k0  1,2
1,2
Единственное целое число, удовлетворяющее данному неравенству, k0 = 1, а его вероятность была получена в примере 7.5.2.
Пример. Сколько раз необходимо подбросить игральную кость, чтобы наивероятнейшее число выпадения тройки было равно 10?
Решение. В данном случае р=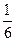 . Согласно неравенству (15):
. Согласно неравенству (15):
п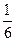 -
- 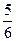
 10
10  п
п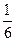 +
+ 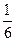 ,
,
п – 5 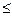 10
10  п + 1,
п + 1,
59 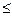 п
п 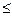 65,
65,
т.е. необходимо подбросить кость от 59 до 65 раз включительно.
|
|
|
|
|
Дата добавления: 2014-10-23; Просмотров: 4019; Нарушение авторских прав?; Мы поможем в написании вашей работы!