Формула полной вероятности.Формула Байеса

Следствием двух основных теорем теории вероятностей - теоремы сложения и теоремы умножения, являются формула полной вероятности и формула Байеса.

Теорема. Если событие А может произойти только при условии появления одного из событий (гипотез) В₁, В₂,…, В_п, образующих полную группу, то вероятность события А равна сумме произведений вероятностей каждого из этих событий (гипотез) на соответствующие условные вероятности события А:

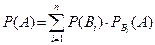(11)

По условию гипотезы В₁, В₂,…, В_п образуют полную группу, следовательно, они единственно возможные и несовместные. Тогда

А = В₁А+В₂А+…+В_пА

По теореме сложения вероятностей

Р(А) = Р(В₁А) + Р(В₂А) + … + Р(В _п А)

По теореме умножения вероятностей для совместных событий

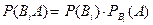, откуда и получается утверждение (11) – формула полной вероятности.

Формула Байеса применяется, когда событие А, которое может появиться только с одной из гипотез В₁, В₂,…, В_п , образующих полную группу, произошло, и необходимо произвести количественную переоценку априорных вероятностей этих гипотез Р(В₁), Р(В₂),…, Р(В_п), известных до испытания, т.е. надо найти апостериорные (получаемые после проведения испытания) условные вероятности гипотез Р_А(В₁), Р_А(В₂),…, Р_А(В_п).

Для получения искомой формулы запишем теорему умножения вероятностей

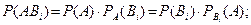откуда

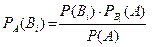или с учетом (11):

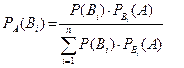(12)

Формула (12) называется формулой Байеса.

Значение формулы Байеса состоит в том, что при наступлении события А, т.е. по мере получения новой информации, мы можем проверять и корректировать выдвинутые до испытания гипотезы. Такой подход, называемый байесовским, дает возможность корректировать управленческие решения в экономике, оценки неизвестных параметров распределения изучаемых признаков в статистическом анализе и т.п.

Пример. В магазин поступила новая продукция с трех предприятий в процентном составе: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия. Известно, что 10% продукции первого предприятия высшего сорта, второго предприятия - 5%, третьего предприятия - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная нами продукция окажется высшего сорта.

Р е ш е н и е. Обозначим события: А – была куплена продукция высшего сорта. В₁, В₂, В₃ – покупка продукции, принадлежащей соответственно первому, второму и третьему предприятию. Очевидно, что событие А может произойти только совместно с одним из событий В₁, В₂ или В₃, т.к. они образуют полную группу, т.е.

А = В₁А+В₂А+В₃А

По формуле полной вероятности

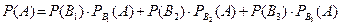
Р(А) = 0,2· 0,1 + 0,3· 0,05 + 0,5· 0,2 = 0,135

Дата добавления: 2014-10-23