Элементы комбинаторики

Для успешного решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики - раздела математики, изучающего, в частности, методы решения комбинаторных задач – задач на подсчет числа различных комбинаций.

Сформулируем два важных правила, часто применяемых для решения комбинаторных задач.

Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов т способами, а другой объект В может быть выбран п способами, то выбрать либо А, либо В можно т+п способами.

Пример. В ящике 300 деталей. Известно, что 150 из них – 1-го сорта, 120 – 2-го сорта, а остальные – 3-го сорта. Сколько существует способов извлечения из ящика одной детали 1-го или второго сорта?

Р е ш е н и е. Деталь 1-го сорта может быть извлечена т=150 способами, а деталь 2-го сорта - п =120 способами. По правилу суммы существует т+п =150 + 120 = 270 способов извлечения одной детали первого или второго сорта.

Правило произведения. Если некоторый объект А может быть выбран из совокупности объектов т способами, и после каждого такого выбора другой объект В может быть выбран п способами, то пара объектов (А;В) в указанном порядке может быть выбрана тп способами.

Пример. В группе 30 человек. Необходимо выбрать старосту, его заместителя и профорга. Сколько существует способов это сделать?

Решение. Старостой может быть выбран любой из 30 учащихся, его заместителем – любой из оставшихся 29, а профоргом - любой из оставшихся 28 учащихся, т.е. т =30, п =29, k =28. По правилу произведения общее число способов выбора старосты, его заместителя и профорга равно mnk =30·29·28=24360 способов.

Пусть дано множество N из п различных элементов.

Перестановками называют комбинации, состоящие из одних и тех же п различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок

Р _п = п! (3)

п! = 1× 2 × …× п, 0! = 1.

Пример. Сколько трехзначных чисел можно составить из цифр 4,5,6, если каждая цифра входит в изображение числа только один раз?

Решение. Искомое число трехзначных чисел

.

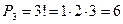Из элементов множества N могут быть образованы подмножества из т элементов (). Например, из 5 элементов a,b,c,d,e могут быть отобраны комбинации по 2 элемента - ab,cd, da, ce и т.д., по 3 элемента - abc, ead, cbd и т.д.

Размещениями называют комбинации, составленные из п элементов по т элементов, которые отличаются либо составом элементов, либо их порядком, либо и тем и другим.

Число всех возможных размещений

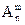= п(п-1)(п-2) …(п-т+1) или 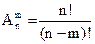(4)

Пример. Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе из 11 дисциплин.

Решение. Каждый вариант расписания представляет набор 5 дисциплин из 11, отличающихся от других вариантов как составом дисциплин, так и порядком их следования (или и тем и другим), т.е. является размещением из 11 элементов по 5. Число вариантов расписаний находим по формуле (4):

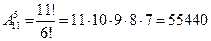
Сочетаниями называют комбинации, составленные из п элементов по т элементов, которые отличаются хотя бы одним элементом. Число сочетаний

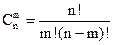(5)

Пример. Сколькими способами можно выбрать две детали из ящика, содержащего деталей?

Решение. Искомое число способов

С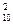 = 10!/ (2! 8!) = 45.

Пример. В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?

Решение. Каждая партия играется двумя участниками из 16 и отличается только составом пар, т.е. представляет собой сочетание из 16 элементов по 2. Их число находим по формуле (5):

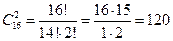
Числа размещений, сочетаний и перестановок связаны равенством:

(6)

Контрольные вопросы и задания для самостоятельной подготовки:

1. Предмет теории вероятностей.

2. Виды случайных событий.

3. Классическое определение вероятности.

4. Основные формулы комбинаторики.

5. Относительная частота.

6. Устойчивость относительной частоты. Статистическое определение вероятности.

7. Вероятность попадания точки в геометрическую область.

8. Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе из 11 дисциплин.

9. В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?

10. При перевозке ящика, в котором содержались 21 стандартная и 10 нестандартных деталей, утеряна одна деталь. Наудачу извлеченная детальоказалась стандартной. Найти вероятность того, что утеряна стандартная деталь.

11. В урне лежат т белых шаров и п черных.Чему равна вероятность вытащить белый шар?

12. Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях равна 7.

13. Десять книг наудачу расставляются на книжной полке. Какова вероятностьтого, что три конкретные из этих десяти книг окажутся стоящими рядом?

14. На отдельных карточках написаны три буквы «а», две буквы «н» и одна буква «с». Ребенок берет карточки в случайном порядке и прикладывает одну к другой все 6 карточек. Какова вероятность того, что получится слово «ананас»?

15. Из 30 студентов 10 имеют спортивные разряды. Какова вероятность того, что выбранные наудачу 3 студента – разрядники?

16. В магазине было продано 21 из 25 холодильников трех марок, имеющихся в количествах 5, 7 и 13 штук. Полагая, что вероятность быть проданным для холодильника каждой марки одна и та же, найти вероятность того, что остались нераспроданными холодильники одной марки.

17. При перевозке ящика, в котором содержались 21 стандартная и 10 нестандартных деталей, утеряна одна деталь, причем неизвестно какая. Наудачу извлеченная деталь оказалась стандартной. Найти вероятность того, что была утеряна стандартная деталь.

18. Брошены две игральные кости. Найти вероятность того, что сумма очков на

выпавших гранях равна десяти.

19. Бросают две игральные кости. Какое событие более вероятно: сумма очков на

выпавших гранях равна 11 или сумма очков на выпавших гранях равна 4?

20. Восемь книг наудачу расставляются на книжной полке. Какова вероятность того, что две конкретные из этих книг окажутся стоящими рядом?

21. В мешочке имеется 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: о,п,р,с,т. Найти вероятность того, что на вынутых по одному и расположенных «в одну линию» кубиков можно будет прочесть слово «спорт».

22. В денежно- вещевой лотерее на каждые 10000 билетов разыгрывается 90 вещевых и 60 денежных выигрышей. Чему равна вероятность выигрыша, безразлично денежного или вещевого, для владельца одного лотерейного билета?

Дата добавления: 2014-10-23