Математическое ожидание

Показательный закон надежности.

Часто длительность безотказной работы элемента имеет показательное распределение, то есть

F (t) = 1 – e^-λt.

Следовательно, функция надежности в этом случае имеет вид:

R (t) = 1 – F (t) = 1 – (1 – e^-λt) = e^-λt.

Определение. Показательным законом надежности называют функцию надежности, определяемую равенством

R (t) = e^-λt,

где λ – интенсивность отказов.

Пример. Пусть время безотказной работы элемента распределено по показательному закону с плотностью распределения f (t) = 0,1 e^{- 0,1 t} при t ≥ 0. Найти вероятность того, что элемент проработает безотказно в течение 10 часов.

Решение. Так как λ = 0,1, R (10) = e ^-0,1·10 = e ^-1 = 0,368.

Определение. Математическим ожиданием дискретной случайной величины называется сумма произведений ее возможных значений на соответствующие им вероятности:

М (Х) = х ₁ р ₁ + х ₂ р ₂ + … + х_пр_п.

Если число возможных значений случайной величины бесконечно, то 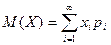, если полученный ряд сходится абсолютно.

Замечание 1. Математическое ожидание называют иногда взвешенным средним, так как оно приближенно равно среднему арифметическому наблюдаемых значений случайной величины при большом числе опытов.

Замечание 2. Из определения математического ожидания следует, что его значение не меньше наименьшего возможного значения случайной величины и не больше наибольше-го.

Замечание 3. Математическое ожидание дискретной случайной величины есть неслучай-ная (постоянная) величина. В дальнейшем увидим, что это же справедливо и для непре-рывных случайных величин.

Пример. Найдем математическое ожидание случайной величины Х – числа стандартных деталей среди трех, отобранных из партии в 10 деталей, среди которых 2 бракованных. Составим ряд распределения для Х. Из условия задачи следует, что Х может принимать значения 1, 2, 3. Тогда

Пример 2. Определим математическое ожидание случайной величины Х – числа бросков монеты до первого появления герба. Эта величина может принимать бесконечное число значений (множество возможных значений есть множество натуральных чисел). Ряд ее распределения имеет вид:

Х			…	п	…
р	0,5	(0,5)^2	…	(0,5) ^п	…

Тогда ..+

+(при вычислении дважды использовалась формула суммы бесконечно убывающей геометрической прогрессии: , откуда ).

Свойства математического ожидания.

1) Математическое ожидание постоянной равно самой постоянной:

М (С) = С.

Доказательство. Если рассматривать С как дискретную случайную величину, принимающую только одно значение С с вероятностью р = 1, то М (С) = С ·1 = С.

2) Постоянный множитель можно выносит за знак математического ожидания:

М (СХ) = С М (Х).

Доказательство. Если случайная величина Х задана рядом распределения

xi	x 1	x 2	…	xn
pi	p 1	p 2	…	pn

то ряд распределения для СХ имеет вид:

Сxi	Сx 1	Сx 2	…	Сxn
pi	p 1	p 2	…	pn

Тогда М (СХ) = Сх ₁ р ₁ + Сх ₂ р ₂ + … + Сх_пр_п = С (х ₁ р ₁ + х ₂ р ₂ + … + х_пр_п) = СМ (Х).

Определение. Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие значения приняла другая. В противном случае случайные величины зависимы.

Определение. Назовем произведением независимых случайных величин Х и Y случайную величину XY, возможные значения которой равны произведениям всех возможных значений Х на все возможные значения Y, а соответствующие им вероят-ности равны произведениям вероятностей сомножителей.

3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

M (XY) = M (X) M (Y).

Доказательство. Для упрощения вычислений ограничимся случаем, когда Х и Y принимают только по два возможных значения:

xi	x 1	x 2
pi	p 1	p 2

уi	у 1	у 2
gi	g 1	g 2

Тогда ряд распределения для XY выглядит так:

ХY	x 1 y 1	x 2 y 1	x 1 y 2	x 2 y 2
p	p 1 g 1	p 2 g 1	p 1 g 2	p 2 g 2

Следовательно, M (XY) = x ₁ y ₁· p ₁ g ₁ + x ₂ y ₁· p ₂ g ₁ + x ₁ y ₂· p ₁ g ₂ + x ₂ y ₂· p ₂ g ₂ = y ₁ g ₁(x ₁ p ₁ + x ₂ p ₂) + + y ₂ g ₂(x ₁ p ₁ + x ₂ p ₂) = (y ₁ g ₁ + y ₂ g ₂) (x ₁ p ₁ + x ₂ p ₂) = M (X)· M (Y).

Замечание 1. Аналогично можно доказать это свойство для большего количества возможных значений сомножителей.

Замечание 2. Свойство 3 справедливо для произведения любого числа независимых случайных величин, что доказывается методом математической индукции.

Определение.Определим сумму случайных величин Х и Y как случайную величину Х + Y, возможные значения которой равны суммам каждого возможного значения Х с каждым возможным значением Y; вероятности таких сумм равны произведениям вероятностей слагаемых (для зависимых случайных величин – произведениям вероятности одного слагаемого на условную вероятность второго).

4) Математическое ожидание суммы двух случайных величин (зависимых или незави-симых) равно сумме математических ожиданий слагаемых:

M (X + Y) = M (X) + M (Y).

Доказательство.

Вновь рассмотрим случайные величины, заданные рядами распределения, приведен-ными при доказательстве свойства 3. Тогда возможными значениями X + Y являются х ₁ + у ₁, х ₁ + у ₂, х ₂ + у ₁, х ₂ + у ₂. Обозначим их вероятности соответственно как р ₁₁, р ₁₂, р ₂₁ и р ₂₂. Найдем М (Х + Y) = (x ₁ + y ₁) p ₁₁ + (x ₁ + y ₂) p ₁₂ + (x ₂ + y ₁) p ₂₁ + (x ₂ + y ₂) p ₂₂ =

= x ₁(p ₁₁ + p ₁₂) + x ₂(p ₂₁ + p ₂₂) + y ₁(p ₁₁ + p ₂₁) + y ₂(p ₁₂ + p ₂₂).

Докажем, что р ₁₁ + р ₂₂ = р ₁. Действительно, событие, состоящее в том, что X + Y примет значения х ₁ + у ₁ или х ₁ + у ₂ и вероятность которого равна р ₁₁ + р ₂₂, совпадает с событием, заключающемся в том, что Х = х ₁ (его вероятность – р ₁). Аналогично дока-зывается, что p ₂₁ + p ₂₂ = р ₂, p ₁₁ + p ₂₁ = g ₁, p ₁₂ + p ₂₂ = g ₂. Значит,

M (X + Y) = x ₁ p ₁ + x ₂ p ₂ + y ₁ g ₁ + y ₂ g ₂ = M (X) + M (Y).

Замечание. Из свойства 4 следует, что сумма любого числа случайных величин равна сумме математических ожиданий слагаемых.

Пример. Найти математическое ожидание суммы числа очков, выпавших при броске пяти игральных костей.

Найдем математическое ожидание числа очков, выпавших при броске одной кости:

М (Х ₁) = (1 + 2 + 3 + 4 + 5 + 6)Тому же числу равно математическое ожидание числа очков, выпавших на любой кости. Следовательно, по свойству 4 М (Х)=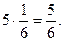

Дата добавления: 2014-10-23