Тема: матричні операції в Excel

Лабораторна робота 7.

(2г.)

Мета: Отримати відомості про матричні операції в Excel та

навчитися застосовувати їх до конкретних задач.

Теоретичні відомості.

Означення 1. Добуток m n – матриці А на n p матрицю В – це така m р – матриця С = А×В, елемент с_ij якої є скалярним добутком вектор – рядка і матриці А на вектор – стовпець j матриці В.

Добуток 2 ´ 3 матриці А = 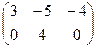на 2 ´ 2 матрицю В = С = А × В не існує, оскільки число стовпців матриці А дорівнює 3 і не дорівнює числу рядків В.

Означення 2. Матриця, обернена до квадратної матриці А порядку n – це така квадратна матриця А^-1 того ж порядку, що А А^-1 = А^-1 А = Е, де Е – одинична матриця.

Якщо А має обернену, то її можна знайти методом Гаусса. Розглянемо n ´ 2n матрицю АЕ, яку можна отримати, дописавши праворуч від матриці А одиничну матрицю того ж порядку. Наприклад, якщо А = 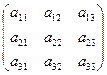, то АЕ = 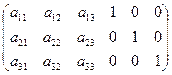. Зведемо матрицю АЕ до діагональної форми методом Гаусса. Тоді вона отримає вигляд ЕВ, де В – деяка квадратна матриця порядку n. Наприклад при n = 3 ЕВ = . Стверджується, що така матриця В і є обернена до А, тобто В = А^-1.

Хід роботи.

Для множення матриць є спеціальний вбудований оператор Excel МУМНОЖ. Наприклад, у наступній електронній таблиці

	A	B	C	D	E	F
		-5				-4
	-7

задані 3 ´ 2 матриця А = 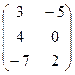і 2 ´ 3 матриця В = 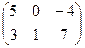. Для знаходження 3 ´ 3 матриці С = А × В виділимо діапазон А5:С7 і (можливо за допомогою вікна цього оператора) введемо в нього формулу = МУМНОЖ(А1:В3;D1:F2):

	A	B	C	D	E	F
		-5				-4
	-7
	=МУМНОЖ(А1:В3;D1:F2)

Після цього, притримуючи кнопки Alt i Shift, треба натиснути не Enter. В результаті отримаємо матрицю С:

	A	B	C	D	E	F
		-5				-4
	-7
		-5	-47
			-16
	-29

Якщо спробувати помножити матриці А і В з нерівними числами стовпців у А та рядків у В, то отримаємо повідомлення про помилку #ЗНАЧ!.

Задача. Знайти матрицю, обернену до матриці А = 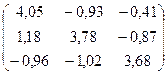методом Гаусса.

Розв’язання. Задамо в електронній таблиці матрицю АЕ:

	A	B	C	D	E	F
	4,05	-0,93	-0,41
	1,18	3,78	-0,87
	-0,96	-1,02	3,68

Зведемо її до діагональної так само, як і в лабораторній роботі 6:

	A	B	C	D	E	F
	4,05	-0,93	-0,41
	1,18	3,78	-0,87
	-0,96	-1,02	3,68
		-0,22963	-0,10123	0,246914
		4,050963	-0,75054	-0,29136
		-1,24044	3,582815	0,237037
			-0,14378	0,230398	0,056685
			-0,18528	-0,07192	0,246855
			3,352991	0,14782	0,30621
				0,236737	0,069816	0,042881
				-0,06376	0,263775	0,055257
				0,044086	0,091324	0,298241

0,236737 0,069816 0,042881

Отже, матриця В = – 0,06376 0,263775 0,055257 є оберненою до матриці А.

0,044086 0,091324 0,298241

Перевірка.

Перевіримо це безпосередньо за означенням за допомогою вбудованого оператора МУМНОЖ. Результат множення А на В, тобто результат дії оператору МУМНОЖ(A1:C3; D13:F15) дорівнює

	-3,46945E-17	-1,38778E-17
6,25E-17		-5,55112E-17
	-5,55112E-17

Оскільки числа ~ 10^-17 з точки зору Excel не відрізняються від нуля, то отримана матриця є одиничною. Знайти обернену матрицю можна також і за допомогою спеціального вбудованого оператора Excel МОБР. Треба виділити квадратний діапазон того ж розміру, що й у даної матриці, (в цьому прикладі з 9 чарунок), задати в ньому цей оператор, єдиним аргументом якого є діапазон даної матриці (тут це МОБР(А1:С3)) і, притримуючи кнопки Alt i Shift, натиснути не Enter.

Дата добавления: 2014-10-31