Лабораторна робота 5

Завдання.

Контрольні питання.

1. З яких етапів складається знаходження наближених коренів рівняння методом Ньютона?
2. В чому полягає алгоритм методу Ньютона?
3. Які передумови необхідно забезпечити для застосування методу Ньютона?
4. Що можна зробити, якщо на відрізку ізоляції кореня знак f′′ (x) змінюється і отже умови застосування методу Ньютона не виконані?
5. Яку точку треба обрати за початкову точку метода Ньютона?
6. Якщо для початкової точки х методу Ньютона виконується умова f (х) ∙ f′′ (х) < 0, то чи можна стверджувати, що не буде збіжності цього методу?
7. Якщо зміна значень послідовних ітерацій методу Ньютона припинилась, то чи є це відповідь, тобто наближений корінь даного рівняння з даною точністю?

Знайти відрізки ізоляції коренів даного рівняння на відрізку [– 10; 10] і розв’язати його на кожному з цих відрізків методом Ньютона з точністю e = 0,5*10^-6.

№	Рівняння
	2^x + 5x – 3 = 0
	x^2+ 4sin x – 1= 0
	x^2- 20sin x – 1= 0
	3x – cos x –1 = 0
	сtg x – 0.5x = 0
	2^x (x-2)^2 – 1 =0
	x^2– cos x= 0
	(x - 3)cos x– 1 = 0
	x^3 – 3x^2 – 24x – 5 =0
	x^3– 2x – 5 = 0

(2г.)

Тема: метод лінійного інтерполювання (метод хорд).

Мета: Отримати відомості про метод хорд обчислення кореня на відрізку ізоляції

з наперед заданою точністю та навчитися застосовувати цей метод до конкретних задач.

Теоретичні відомості.

Це класичний ітераційний метод наближеного обчислення кореня рівняння f (x) = 0 на відрізку його ізоляції [a;b]. Цей метод визначає формула

х_k+1 = х_k – 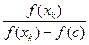(х_k – с) (k = 0, 1, 2, …),

де с Î [a;b]. Для застосування методу лінійного інтерполювання необхідно забезпечити наступні передумови.

1. Треба знайти відрізок ізоляції шуканого кореня.

2. Треба забезпечити, щоби на відрізку ізоляції не змінювалися знаки у першої та другої похідних, зменшуючи при необхідності початковий відрізок.

3. За початкове наближення можна брати будь – яку точку х відрізку ізоляції, у якій виконується умова f (х) ∙ f′′ (х) < 0.

4. За нерухомий кінець с, який входить до формули методу, можна взяти будь – яку точку відрізку ізоляції, у якій виконується умова f (с) ∙ f′′ (с) > 0.

Хід роботи.

Задача. Р озв‘язати рівняння f (x) = 2^х + 5x – 3 = 0 на відрізку [– 10; 10] з точністю e = 0,5*10^-5 методом лінійного інтерполювання.

1. Відокремлення коренів рівняння на відрізку [– 10; 10].

Ця задача уже була розв’язана у лабораторній роботі 2 і там був знайдений відрізок ізоляції [0;1] для єдиного кореня даного рівняння.

2. Умови застосовування методу.

Незмінність знаку першої похідної була перевірена в лабораторній роботі 2 при всіх х. Друга похідна f′′ (х) = 2^х(ln 2)² > 0 при всіх х. Отже на [0;1] знак f′′ (х) не змінюється.

3. Початкове наближення.

Оскільки f (0) = – 2, звідки f (0) ∙ f′′ (0) < 0, то за початкове наближення можна взяти точку а = 0.

4. Нерухомий кінець методу.

Оскільки f (1) = 4, звідки f (1) ∙ f′′ (1) > 0, то за нерухомий кінець с з формули методу можна взяти точку b = 1.

5. Знайдемо корінь на відрізку ізоляції з точністю e = 0,5*10^-5 методом лінійного інтерполювання.

Надамо чарункам електронної таблиці таких значень:

	A	B	C	D
		= 2^A1 + 5*A1 – 3		= 2^C1 + 5*C1 – 3
	= A1 – B1*(A1 – $C$1)/(B1 – $D$1)	↓
	↓	↓

Тут у чарунці А1 початкове наближення а = 0, у В1 f (a), у C1 нерухомий кінець b = 1, у D1 f (b). Зауважимо, що формулу у D1 можна просто скопіювати з В1. У чарунці А2 задана формула методу лінійного інтерполювання. Нерухомий кінець не змінюється, отже для його завдання використана абсолютна адресація (після набору С1 треба натиснути F4; так само з D1). Формули у стовбцях А і В копіюються. В результаті отримуємо:

	A	B	C	D
		-2
	0,333333333	-0,073412283
	0,345348204	-0,0028014
	0,345806369	-0,000107047
	0,345823876	-4,09071E-06
	0,345824545	-1,56323E-07
	0,34582457	-5,97374E-09
	0,345824571	-2,28281E-10
	0,345824571	-8,72369E-12
	0,345824571	-3,33067E-13

Для стабілізації знадобилось 8 ітерацій при максимально можливому для комп’ютера числі значущих цифр у чарунці. Це ефект обчислювальної похибки, докладно розглянутий у [2].

Перевірка.

Перевіримо правильність отриманого розв’язку безпосередньо. А саме надамо чарункам таких значень:

	A	B	C
	= А10 + 0,5*10^-^5
	= А10 – 0,5*10^-^5

У стовпці В значення функції f (x) приймаються автоматично. В результаті отримаємо:

	A	B	C	D
	0,345824571	-3,33067E-13
	0,345829571	2,94045E-05
	0,345774571	-0,000294044

Оскільки f (0,345824571 + 0,5*10^-5) > 0, a f (0,345824571 – 0,5*10^-5) < 0, то відмінність значення 0,345824571 від точного значення кореня не перевищує e = 0,5*10^-5, тобто це значення є єдиним коренем рівняння f (x) = 0 з точністю 0,5*10^-5.

Дата добавления: 2014-10-31