Тема: відокремлення коренів

Мета: Отримати відомості про методи відокремлення коренів рівняння з одною

змінною на відрізку множини дійсних чисел.

Теоретичні відомості.

Нехай задано рівняння з одною змінною , де функція визначена і неперервна на деякому відрізку [a;b] множини дійсних чисел.

Означення 1. Розв‘язати рівняння означає знайти множину всіх його коренів (тобто таких значень х є [a;b], при яких воно стає числовою тотожністю) або ж довести, що їх не існує. Розв‘язок (корінь) рівняння 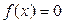називають ще нулем функції .

В чисельних методах рівняння вважається розв‘язаним, якщо всі корені знайдені з заданою точністю, тобто з наперед заданою похибкою.

Означення 2. В ідрізком ізоляції кореня рівняння називають такий відрізок множини дійсних чисел, в якому рівняння має один і тільки один розв‘язок.

Знаходження наближених коренів рівняння звичайно складається з двох етапів:

1) відокремлення коренів, тобто знаходження для кожного з них відрізку ізоляції;

2) обчислення кореня у відрізку ізоляції з наперед заданою точністю.

Для знаходження відрізків ізоляції застосовуються методи графічні, аналітичні та деякі їх комбінації. Найпростіше скористатися графічним методом: можна побудувати графік функції за допомогою Майстра діаграм Excel і знайти відрізки ізоляції з графіку та з таблиці даних, за якою цей графік побудований.

Проте, отримані так результати не є обґрунтованими, не завжди є правильними. Точні результати ґрунтуються на такому відомому твердженні математичного аналізу.

Теорема 1. Якщо функція 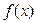неперервна на [ a;b ] і набуває на кінцях цього відрізка значень протилежних знаків, тобто f(a)* f(b) < 0, то на відрізку існує хоча б один корінь рівняння f (x) = 0.

2. Якщо при цьому f (x) має першу похідну, яка зберігає сталий знак всередині відрізка [ a;b ], то рівняння на цьому відрізку має єдиний корінь.

Аналітичний метод відокремлення коренів для рівняння f (x) = 0 з диференційовною функцією f (x) полягає в тому, щоб

1. Знайти критичні точки функції f (x).
2. Знайти інтервали монотонності функції f (x) (це інтервали між критичними точками. На інтервалі монотонності не більш як один корінь за теоремою 2).
3. Інтервал монотонності містить корінь функції f (x), якщо f (x) набуває на кінцях цього інтервалу значень протилежних знаків (за теоремою 1).
4. Відрізки ізоляції коренів (бажано якнайменші) обрати так, щоби кожний з них містив корінь і містився у відповідному інтервалі монотонності.

На жаль, приклади рівнянь, до яких можна застосувати аналітичний метод поодинокі. Тому для таких рівнянь доречним є комбінований метод:

1. У таблиці значень функції f (x) (за допомогою відповідного графіка) знайти відрізки зміни знака цих значень (бажано якнайменші). На кожному такому відрізку існує корінь рівняння f (x) = 0(за теоремою 1).
2. Побудувати таблицю значень похідної f ′(x) і відповідний графік.
3. Якщо на відрізку зміни знака функції f (x) з пункту 1 похідна f ′(x) не змінює знака, то на ньому єдиний корінь (за теоремою 2), тобто це відрізок ізоляції кореня.
4. Якщо на відрізку зміни знака функції f (x) змінює знак і похідна f ′(x), то треба повернутись до пункту 1 і зменшити відрізки зміни знаку функції f (x).

Комбінованийметод може бути застосований до довільного рівняння f (x) = 0 з диференційовною функцією f (x). У повному обсязі він є точним [2].

Хід роботи.

Задача 1. Відокремити корені рівняння 2sinx – x² + 2 = 0 на відрізку [– 2; 3] графічним методом.

Побудуємо графік функції у = 2sinx – x² + 2 Майстром діаграм Excel за наступною електронною таблицею, де у стовпці А точки з відрізку [– 2; 3], у стовпці В – значення функції у = 2sinx – x² + 2 у цих точках.

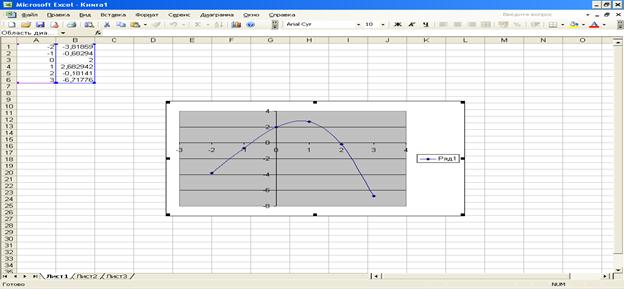
А саме, виділимо діапазон А1:В6, оберемо Мастер диаграмм – Точечная – Точечная диаграмма со значениями, соединёнными сглаживающими линиями та натиснемо на Готово. Можна побачити безпосередньо, що точки перетину графіку з віссю абсцис, тобто корені рівняння 2sinx – x² + 2 = 0 – це приблизно точки – 0,8 і 2. Це підтверджується і відповідною електронною таблицею: значення функції у стовпці В змінюють знак на відрізках [– 1; 0] та [1; 2]. У якості можливих відрізків ізоляції оберемо саме ці відрізки.

Інший варіант графічного методу.

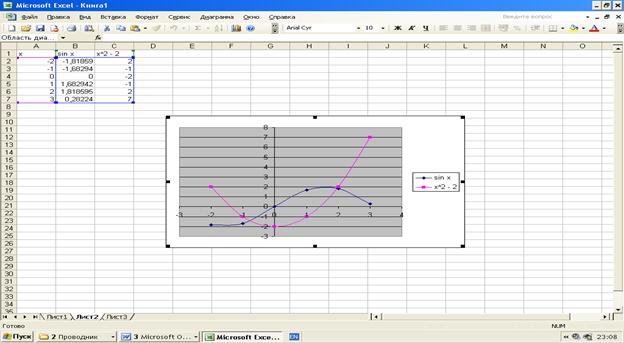
Запишемо рівняння 2sinx – x² + 2 = 0 у вигляді , де φ(х) = 2sinx, g(x) = = x² – 2 і побудуємо графіки функцій 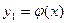і 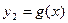так само, як і вище.

Як бачимо, перетин графіків функцій φ(х) = 2sinx та g(x) = x² – 2 – це точки на відрізках [– 1; 0] та [1; 2]. Саме ці відрізки оберемо у якості можливих відрізків ізоляції.

Задача 2. Відокремити корені рівняння sinx – x + 1 = 0 на відрізку [1; 3] аналітичним методом.

Графік функції f (x) = sinx – x + 1 на відрізку [1; 3] побудуємо так само, як і в попередній задачі; виглядає він так.

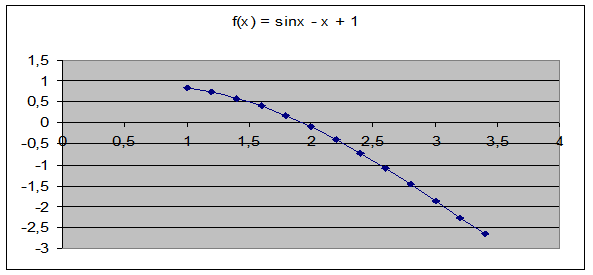
Застосуємо для знаходження відрізків ізоляції аналітичний метод.

1. Критичні точки – це розв’язки рівняння f ′(x) = cos x – 1 = 0. Отже, cos x = 1, критичні точки x = 2πk (k є Z).

2. Оскільки │cos x│≤ 1, то f ′(x) ≤ 0, до того ж f ′(x) < 0 у всіх точках окрім критичних. Це означає, що вся вісь є інтервалом монотонності f (x). Отже, згідно з теоремою 2, існує, як максимум, один корінь даного рівняння.

3. Згідно з графіком корінь приблизно дорівнює 2; згідно з таблицею, за якою побудований графік, значення функції змінюють знак на відрізку [1,8; 2]: f (1,8) > 0, f (2) < 0. Отже, на цьому відрізку є корінь рівняння згідно з теоремою 1.

4. У якості відрізка ізоляції цього кореня можна обрати довільний відрізок, що містить його, скажімо [1,8;2,2] (бажано, щоб він був якнайменше).

Додатково з 2. і 3. випливає, що існує єдиний корінь даного рівняння не тільки на [1; 3], але й на всій дійсній прямій.

Задача 3. Знайти відрізки ізоляції коренів рівняння f (x) = 2sinx – x² + 2 на відрізку [– 2; 3] комбінованим методом відокремлення коренів.

1. Побудуємо таблицю значень та графік функції у = 2sinx – x² + 2 Майстром діаграм Excel так само, як у задачі 1.

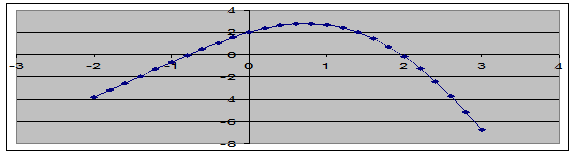
Згідно з таблицею та графіком відрізками зміни знака функції f (x) є відрізки [– 1; 0] та [1; 2].

2. Похідна f ′(x) = 2 ∙ cos x – 2х, відповідний графік наступний.

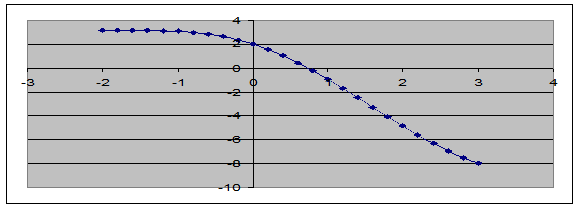
3. На відрізку [– 1; 0] f ′(x) > 0 (тобто f (x) зростає), на відрізку [1; 2] f ′(x) < 0, (тобто f (x) спадає). Отже, на обох відрізках зміни знака функції f (x) похідна f ′(x) знака не змінює, тому обидва є відрізками ізоляції коренів рівняння.

Дата добавления: 2014-10-31