Тема: метод Гаусса розв’язування систем лінійних рівнянь

Лабораторна робота 6.

Завдання.

Контрольні питання.

1. З яких етапів складається знаходження наближених коренів рівняння методом лінійного інтерполювання?
2. В чому полягає алгоритм методу хорд?
3. Які передумови необхідно забезпечити для застосування методу хорд?
4. Що можна зробити, якщо на відрізку ізоляції кореня знак f′ (x) або f′′ (x) змінюється і отже умови застосування методу хорд не виконані?
5. Яку точку треба обрати за початкову точку метода Ньютона?
6. Яку точку треба обрати занерухомий кінець методу лінійного інтерполювання?
7. Якщо для початкової точки х методу Ньютона виконується умова f (х) ∙ f′′ (х) > 0, то чи можна стверджувати, що не буде збіжності цього методу?
8. Якщо зміна значень послідовних ітерацій методу Ньютона припинилась, то чи є це відповідь, тобто наближений корінь даного рівняння з даною точністю?

Знайти відрізки ізоляції коренів даного рівняння на відрізку [– 10; 10] і розв’язати його на кожному з цих відрізків методом Ньютона з точністю e = 0,5*10^-6.

№	Рівняння
	2^x + 5x – 3 = 0
	x^2+ 4sin x – 1= 0
	x^2- 20sin x – 1= 0
	3x – cos x –1 = 0
	сtg x – 0.5x = 0
	2^x (x-2)^2 – 1 =0
	x^2– cos x= 0
	(x - 3)cos x– 1 = 0
	x^3 – 3x^2 – 24x – 5 =0
	x^3– 2x – 5 = 0

Література:

1. Бахвалов Н.С. Численные методы – М: Наука, 1973. т. 1. – 631с.
2. Вейцбліт О.Й. Основи чисельних методів математики (з використанням Excel) – Херсон: Видавництво ХДУ, 2011. – 280 с.
3. Лященко М.Я., Головань М.С., Чисельні методи – К: Либідь, 1996 – 288с.

(2г.)

Мета: Отримати відомості про метод Гаусса розв’язування систем лінійних

рівнянь та навчитися застосовувати ці методи до конкретних задач.

Теоретичні відомості.

Метод послідовного виключення змінних, відомий як метод Гаусса, є найпоширенішим методом розв’язання систем лінійних рівнянь (СЛР). Метод Гаусса дозволяє розв’язати будь – яку СЛР в результаті цілком визначеної послідовності елементарних операцій і отже це алгоритм, який можна застосувати на комп’ютері.

Елементарні операції над СЛР:

1. Переміна місцями двох рівнянь.
2. Множення обох частин рівняння на деяке число, відмінне від нуля.
3. Додавання (або віднімання) до обох частин деякого рівняння відповідних частин іншого рівняння, помножених на деяке число.

Елементарним операціям СЛР відповідають

Елементарні операції над матрицею:

1. Переміна місцями двох рядків матриці.
2. Множення рядка матриці на деяке число, відмінне від нуля.
3. Додавання (або віднімання) до рядка іншого рядка, помноженого на деяке число.

Легко перевірити, що в результаті кожної елементарної операції завжди отримується СЛР, еквівалентна (рівносильна) початковій.

Хід роботи.

Задача 1. Розв’язати СЛР .

Розв’язання. Запишемо розширену матрицю даної СЛР у діапазон А2:С4

	A	B	C	D
	x1	x2	x3	b
	3,9	1,25	-0,98	4,905
	0,74	3,45	-0,84	6,031
	-0,65	1,18	2,38	10,134

Тут і надалі доцільно підкреслити всі границі цієї таблиці, натиснувши кнопку Границы → Все границы на панелі Форматирование: це дасть змогу не рахувати потім номер рядка чи стовпця при подальших обчисленнях. На першому кроці алгоритму наша мета – досягти того, щоби в результаті послідовності елементарних операцій над матрицею під рядком 2 у стовпці А значення чарунок дорівнювали нулю. Це і реалізує така електронна таблиця:

	A	B	C	D
	= A2/$A$2	→	→	→
	= A3 – A6*$A$3	→	→	→
	= A4 – A6*$A$4	→	→	→

Тут формули для матричних операцій над рядком записуються в одну чарунку, а потім розповсюджуються на весь рядок, просто перетягнувши маркер заповнення згідно з правилами Excel. Ф ормули треба виконувати спочатку у першому стовпці (у стовпці 6), а потім у стовпцях 7 і 8. В результаті дістанемо:

	A	B	C	D
		0,320513	-0,25128	1,257692
		3,212821	-0,65405	5,100308
		1,388333	2,216667	10,9515

На другому кроці треба отримати 1 для елемента матриці, відповідного В7 і 0 для елементів, відповідних В6 і В8. Це реалізує така електронна таблиця:

	A	B	C	D
	←	= B6 – B11*$B$6	→	→
	←	= B7/$B$7	→	→
	←	= B8 – B11*$B$8	→	→

Тут формули для матричних операцій записуються у чарунки стовпця В, а потім копіюються на відповідні рядки. Ф ормули треба виконувати спочатку у другому стовпці (тобто у стовпці 11), а потім у стовпцях 10 і 12. В результаті дістанемо:

	A	B	C	D
			-0,18603	0,748883
			-0,20358	1,587486
			2,499297	8,74754

Нарешті, на третьому кроці треба отримати 1 для елемента матриці, відповідного С12 і 0 для елементів, відповідних С10 і С11.

	A	B	C	D
	←	←	= C10 – C16*$C$10	→
	←	←	= C11 – C16*$C$11	→
	←	←	= C12/$C$12	→

Формули треба виконувати спочатку у рядку 12, а потім у 10 і 11. В результаті

	A	B	C	D
				1,4
				2,3
				3,5

Матриця системи зведена до діагональної форми. Отже, відповідна СЛР має вигляд: . Це і є розв’язок даної СЛР.

Перевірка.

Перевіримо правильність отриманого розв’язку безпосередньо. А саме виділимо діапазон А18:С18, у чарунці А18 задамо формулу = ТРАНСП(D14:D16). Розв’язок з’явиться у діапазоні А18:С18. Формулу = СУММПРОИЗВ($A$18:$C$18; A2:C2), яка підраховує результат підстановки розв’язку у перше рівняння системи, задамо у чарунці D18. Після цього перетягнемо маркер заповнення з D18 на дві чарунки вниз – там з’являться підрахунки результатів підстановки у друге та третє рівняння розв’язку згідно з правилами копіювання формул в Excel:

	A	B	C	D
	1,4	2,3	3,5	4,905
				6,031
				10,134

Значення в діапазоні D18:D20 точно співпадають з вільними членами даної СЛР у D2:D4, що є безпосереднім доведенням правильності отриманого розв’язку.

Задача 2. Розв’язати СЛР х₁ – 2х₂ + 3х₃ – 2х₄ = 3

2х₁ – 3х₂ + х₃ – 2х₄ = – 2

4х₁ – х₂ + 2х₃ – х₄ = 0.

Розв’язання. Запишемо розширену матрицю даної СЛР у діапазон А2:Е4

	A	B	C	D	Е
	x1	x2	x3	x4	b
		-2		-2
		-3		-2	-2
		-1		-1

– це система трьох лінійних рівнянь з чотирма змінними. Проте метод Гаусса – алгоритм, який дозволяє розв’язати будь – яку СЛР. Послідовність дій фактично не відрізняється від попереднього прикладу. Перший крок:

	A	B	C	D	E
	= A2	→	→	→	→
	= A3 – A6*$A$3	→	→	→	→
	= A4 – A6*$A$4	→	→	→	→

В результаті:

	A	B	C	D	Е
		-2		-2
			-5		-8
			-10		-12

Другий крок:

	A	B	C	D	E
	←	= B6 + B7*2	→	→	→
	←	= В7	→	→	→
	←	= B6 – B7*7	→	→	→

Тут елементи матриці – цілі числа, тому зручно у формулах замість адреси чарунки використати саме значення. В результаті:

	A	B	C	D	Е
			-7		-13
			-5		-8
				-7

Третій крок:

	A	B	C	D	E
	←	←	= C10 – C16*$C$10	→	→
	←	←	= C11 – C16*$C$11	→	→
	←	←	= C12/$C$12	→	→

звідки

	A	B	C	D	Е
				0,04	-0,68
				0,6	0,8
				-0,28	1,76

Матриця у діапазоні А14:С16 зведена до діагонального вигляду, що завершує алгоритм. Отриманій матриці відповідає така СЛР: . Тут за означенням змінні х₁, х₂, х₃, яким відповідають діагональні елементи матриці – це основні (базові) змінні, всі інші (тут тільки х₄) – неосновні (вільні). Переносимо у рівняннях СЛР вільні змінні зліва направо: і отримуємо загальний розв’язок: кожному значенню вільної змінної відповідає свій (частковий) розв’язок і всі розв’язки СЛР мають такий вигляд. В електронній таблиці їх можна отримувати так:

	A	B	C	D	Е	F
				0,04	– 0,68	= E14 – D14*$F$17
				0,6	0,8	↓
				– 0,28	1,76	↓
						*

У чарунку F17 замість * можна занести довільне значення змінної х₄ і в діапазоні F14:F17 дістанемо відповідний частковий розв’язок даної СЛР. Наприклад,

	A	B	C	D	Е	F
				0,04	-0,68	-0,72
				0,6	0,8	0,2
				-0,28	1,76	2,04

або

	A	B	C	D	Е	F
				0,04	-0,68	-0,6
				0,6	0,8
				-0,28	1,76	1,2
						-2

Перевірка.

Перевіримо правильність отриманого розв’язку безпосередньо. А саме виділимо діапазон А19:D19, у чарунці А19 задамо формулу = ТРАНСП(F14:F16). Розв’язок з’явиться у діапазоні А19:D19. Формулу = СУММПРОИЗВ($A$19:$D$19;A2:D2), яка підраховує значення результату підстановки розв’язку у перше рівняння задамо у чарунці Е19 і перетягнемо маркер заповнення на дві чарунки вниз – там з’являться підрахунки результатів підстановки у друге та третє рівняння розв’язку згідно з правилами копіювання формул в Excel:

	A	B	C	D	Е
	-0,6		1,2	-2
					-2
					-4,4E-16

Значення в діапазоні Е19:Е21 співпадають з вільними членами даної СЛР: у чарунці Е14 тут знаходиться значення, яке з точки зору Excel не відрізняється від нуля. Можна надати довільне значення вільній змінній х₄ у чарунці F17: тоді дістанемо новий розв’язок у діапазоні А19:D19, проте значення вільних членів у діапазоні Е19:Е21 залишаться незмінними, що й є безпосереднім доведенням правильності отриманого розв’язку.

Отже, відповідь: – це загальний розв’язок СЛР, або 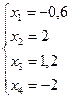– це приклади часткових розв’язків.

Задача 3. Розв’язати СЛР 3х₁ – 2х₂ + х₃ = 2

2х₁ – 3х₂ + 2х₃ = –1

х₁ – х₂ + 3х₃ = 0

2х₁ – 4х₂ + 2х₃ = 3.

Розв’язання. Запишемо розширену матрицю даної СЛР у діапазон А2:D5

	A	B	C	D
	x1	x2	x3	b
		-2
		-3		-1
		-1
		-4

– це система чотирьох лінійних рівнянь з трьома змінними. Але оскільки метод Гаусса – алгоритм, то послідовність дій та ж, що й у попередніх прикладах. Перший крок:

	A	B	C	D
	= A2/$A$2	→	→	→
	= A3 – A7*$A$3	→	→	→
	= A4 – A7*$A$4	→	→	→
	= A5 – A7*$A$5	→	→	→

В результаті:

	A	B	C	D
		- 2/3	1/3	2/3
		-1 2/3	1 1/3	-2 1/3
		- 1/3	2 2/3	- 2/3
		-2 2/3	1 1/3	1 2/3

Оскільки елементи початкової матриці цілі числа, то обрано дрібний формат чарунок.

Другий крок:

	A	B	C	D
	←	= B7 – B13*$B$7	→	→
	←	= B8/$B$8	→	→
	←	= B9 – B13*$B$9	→	→
	←	= B10 – B13*$B$10	→	→

звідки

	A	B	C	D
			- 1/5	1 3/5
			- 4/5	1 2/5
			2 2/5	- 1/5
			- 4/5	5 2/5

Третій крок:

	A	B	C	D
	←	←	= C12 – C19*$C$12	→
	←	←	= C13 – C19*$C$13	→
	←	←	= C14/$C$14	→
	←	←	= C15 – C19*$C$15	→

звідки

	A	B	C	D
				1 7/12
				1 1/3
				- 1/12
				5 1/3

Матриця у діапазоні А17:С19 зведена до діагонального вигляду, що завершує алгоритм. Отриманій матриці відповідає така СЛР: . Останнє рівняння виписано із всіма нульовими коефіцієнтами. Яким би не був набір значень х₁, х₂ , х₃, в результаті їх підстановки в останнє рівняння отримаємо протиріччя: 0 = 5 1/3. Отже, це рівняння, а тому і вся система не мають розв’язків. Але звідси несумісною є й початкова СЛР, еквівалентна кінцевій.

Відповідь: розв’язків не існує.

Дата добавления: 2014-10-31