Тема: інтерполяція функцій

Лабораторна робота 9.

Завдання.

Контрольні питання.

1. Чи для кожної СЛР можна застосувати метод простої ітерації?
2. Чи справді метод простої ітерації не буде збігатися, якщо не виконується умова ô a _iiô > 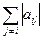для матриці A = (a _ij) СЛР Aх = b?
3. Чи справді СЛР Aх = b завжди має єдиний розв’язок, якщо для матриці A = (a _ij) виконується умова ô a _iiô > ?
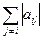4. Чи є необхідним для збіжності методу простої ітерації за початкове наближення обрати b', як це зроблено в задачі?
5. Які вектори можна обирати за початкове наближення х₀ для збіжності методу простої ітерації?
6. Чи всі розв’язки даної СЛР отримані в задачі?

Задача. Розв’язати дану CЛР Aх = b методом простої ітерації. Переконатись у

правильності отриманого розв’язку.

Варіант	Матриця А	b
	3.90	1.25	-0.98	4.905
	0.74	3.45	-0.84	6.031
	-0.65	1.18	2.38	10.134
	2.68	-0.68	0.48	3.868
	-0.73	2.92	-0.39	4.329
	-0.58	-1.12	3.12	7.532
	2.50	-0.91	-0.32	0.287
	-0.91	3.64	-0.48	5.418
	0.48	-0.98	2.14	5.908
	3.45	0.78	-0.97	3.229
	0.78	2.63	-0.89	4.026
	-0.97	-0.89	2.41	5.030
	3.21	0.81	-0.93	3.102
	0.81	2.49	-0.94	3.571
	-0.93	-0.94	2.53	5.391
	2.78	0.38	-0.43	3.261
	-0.78	3.14	-0.81	3.295
	-0.45	-0.86	2.48	6.072
	3.96	-0.78	-0.35	2.525
	1.18	3.78	-0.87	7.301
	-0.96	-1.02	3.68	9.190
	3.48	1.12	-0.94	4.158
	1.08	3.67	-0.87	6.908
	-1.21	-1.43	4.14	9.507
	3.67	0.68	-1.21	2.467
	0.68	2.71	-0.96	3.825
	-1.21	-0.96	2.69	5.513
	3.78	0.67	-0.83	3.928
	0.67	2.76	-0.69	4.871
	-0.83	-0.69	2.39	5.616

Література:

1. Бахвалов Н.С. Численные методы – М: Наука, 1973. т. 1. – 631с.
2. Вейцбліт О.Й. Основи чисельних методів математики (з використанням Excel) – Херсон: Видавництво ХДУ, 2011. – 196 с.
3. Лященко М.Я., Головань М.С., Чисельні методи – К: Либідь, 1996 – 288с.

(2г.)

Мета: Отримати відомості про методи інтерполювання функцій та навчитися

застосовувати ці методи до конкретних задач.

Теоретичні відомості.

Означення 1. Задачею інтерполяції (або інтерполювання) є побудова такої функції, яка для даних значень аргументу приймає задані значення. Нехай для значень аргументу х₁, х₂, …, х_n, які називають вузлами інтерполяції, відомі значення деякої функції f (x): f (x₀) = у₀, f (x₁) = у₁, …, f (x_n) = у_n. Треба знайти інтерполюючу функцію Р(х), так, щоби у вузлах інтерполяції вона приймала ті ж самі значення, що й f (x), тобто Р(x₀) = у₀, Р(x₁) = у₁, …, Р(x_n) = у_n.

Многочлен Р_n(х), який задовольняє умови Р_n(х_i) = y_i = f (x_i) (i = 0, 1, …, n) називають інтерполяційним многочленом.

Означення 2. Наближену рівність f (x) ≈ Р_n(х) називають інтерполяційною формулою.

Означення 3. Поділена різниця нульового порядку f (x_і) співпадає із значенням функції f (x_і). Поділені різниці першого порядку визначаються рівністю f (x_і; x_j) = 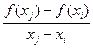, різниці другого порядку – рівністю f (x_і; x_j; x_k) = , …, різниці k – го порядку визначаються через різниці (k – 1) – го порядку за формулою:

f (x₀; x₁; …; x_k) = .

Означення 4. Інтерполяційний многочлен у формі

L_n(x) = f (x₀) + f (x₀; x₁)(х – х₀) + … + f (x₀; x₁;…; x_n)(х – x₀)(х – x₁) … (х – х_n-1)

називають інтерполяційним многочленом Ньютона з поділеними різницями.

Наближену рівність

f (x) ≈ f (x₀) + f (x₀; x₁)(х – х₀) + … + f (x₀; x₁;…; x_n)(х – x₀)(х – x₁) … (х – х_n-1)

називають інтерполяційною формулою Ньютона з поділеними різницями.

Означення 5. Якщо функція f (x) задана у точках x₀, x₁,…, x_n, то таблицю

f (x0)	f (x0; x1)	f (x0; x1; x2)	f (x0; x1; x2; x3)	…	f (x0; x1;…; xn)
f (x1)	f (x1; x2)	f (x1; x2; x3)	f (x1; x2; x3; x4)	…
f (x2)	f (x2; x3)	f (x2; x3; x4)	f (x2; x3; x4; x5)
…	…	…
f (xn-2)	f (xn-2; xn-1)	f (xn-2; xn-1; xn)
f (xn-1)	f (xn-1; xn)
f (xn)

називають таблицею її поділених різниць.

Хід роботи.

Задача 1. Для функції f, заданої таблицею

i
xi	0,45	0,32	0,79	0,51	0,64
yi	0,434966	0,314567	0,710353	0,488177	0,597195

знайти її поділені різниці f (x₂; x₃; x₄), f (x₁; x₂; x₃; x₄), f (x₀; x₁; x₂; x₃; x₄).

Розв’язання. Побудуємо таблицю поділених різниць, звідки й отримаємо шукані значення. Спочатку дістанемо таблицю різниць вузлів інтерполяції x_j – x_i, на які треба ділити поділені різниці за означенням 3. Надамо чарункам електронної таблиці таких значень:

	A	B	C	D	E	F
		xi
	х0	0,45	= В3 – В2	= В4 – В2	= В5 – В2	= В6 – В2
	х1	0,32	↓	↓	↓
	х2	0,79	↓	↓
	х3	0,51	↓
	х4	0,64

Як і раніше, символ ↓ означає копіювання попередніх чарунок. Тут у рядку вузла інтерполяції xi завжди віднімається саме x_i від x_j, а число у заголовку стовпця дорівнює j – i. В результаті отримаємо таку трикутну таблицю:

	A	B	C	D	E	F
		xi
	х0	0,45	-0,13	0,34	0,06	0,19
	х1	0,32	0,47	0,19	0,32
	х2	0,79	-0,28	-0,15
	х3	0,51	0,13
	х4	0,64

Використовуючи цю таблицю, побудуємо тепер трикутну електронну таблицю поділених різниць. Надамо чарункам таких значень:

	A	B	C	D	E	F
	х0	0,434966	=(B11 – B10)/C2	→	→	→
	х1	0,314567	↓	↓	↓
	х2	0,710353	↓	↓
	х3	0,488177	↓
	х4	0,597195

У стовпці B тут значення функції f, задані умовою задачі. Правила копіювання Excel дозволяють отримати у відповідних чарунках саме ті формули, які повинні там бути згідно з означенням 5. В результаті отримаємо:

	A	B	C	D	E	F
	х0	0,434966	0,926146	-0,2472	-0,14442	0,021447
	х1	0,314567	0,842099	-0,25586	-0,14034
	х2	0,710353	0,793486	-0,30077
	х3	0,488177	0,838601
	х4	0,597195

Тут число у заголовку стовпця дорівнює порядку поділеної різниці. У кожному рядку у формулах поділених різниць вузли інтерполяції починаються з того, що знаходиться у заголовку рядка. Так f (x₂; x₃; x₄) є різницею порядку 2 і її формула починається з x₂; отже, ця різниця знаходиться у чарунці D12 і дорівнює – 0,30077. Аналогічно f (x₁; x₂; x₃; x₄) = – 0,14034 і знаходиться у чарунці Е11; f (x₀; x₁; x₂; x₃; x₄) = 0,021447 у чарунці F10.

Зазначимо, що скажімо поділеної різниці f (x₀; x₁; x₃; x₄) нема у цій таблиці: у цій формулі вузли інтерполяції не ідуть підряд, пропущений вузол x₂. Щоби отримати таку різницю треба будувати іншу таблицю, у якій вузли x₀; x₁; x₃; x₄ розташовані підряд.

Задача 2. Додати до таблиці задачі 1 ще один вузол х₅ = 0,49 із значенням функції y₅ = f (0, 49) = 0,470626 і отримати інтерполяційну формулу Ньютона з поділеними різницями для функції f, заданої такою таблицею.

Розв’язання. Після додавання нового вузла маємо таку таблицю:

i
xi	0,45	0,32	0,79	0,51	0,64	0,49
yi	0,434966	0,314567	0,710353	0,488177	0,597195	0,470626

Тут нема потреби будувати все спочатку, можна дописати відповідні рядки та стовпці до уже отриманих у задачі 1 таблиць. Отже, спочатку додамо останні рядок і стовпець до таблиці різниць вузлів інтерполяції x_j – x_i попередньої задачі і продовжимо копіювання на нову діагональ отриманої там трикутної таблиці:

	A	B	C	D	E	F	G
		xi
	х0	0,45	=В3 – В2	=В4 – В2	=В5 – В2	=В6 – В2	=В7 – В2
	х1	0,32	↓	↓	↓	↓
	х2	0,79	↓	↓	↓
	х3	0,51	↓	↓
	х4	0,64	↓
	х5	0,49

В результаті дістанемо:

	A	B	C	D	E	F	G
		xi
	х0	0,45	-0,13	0,34	0,06	0,19	0,04
	х1	0,32	0,47	0,19	0,32	0,17
	х2	0,79	-0,28	-0,15	-0,3
	х3	0,51	0,13	-0,02
	х4	0,64	-0,15
	x5	0,49

Так само додамо рядок, стовпець і продовжимо копіювання на нову діагональ для електронної трикутної таблиці поділених різниць задачі 1. В результаті отримаємо:

	A	B	C	D	E	F	G
	х0	0,434966	0,926146	-0,2472	-0,14442	0,021447	0,007165
	х1	0,314567	0,842099	-0,25586	-0,14034	0,021734
	х2	0,710353	0,793486	-0,30077	-0,13665
	х3	0,488177	0,838601	-0,25978
	х4	0,597195	0,843797
	х5	0,470626

У порівнянні з таблицею поділених різниць задачі 1 тут додатково підрахована поділена різниця порядку 5 f (x₀; x₁; x₂; x₃; x₄; х₅) = 0,007165. Тепер треба виписати інтерполяційну формулу Ньютона:

f (x) ≈ f (x₀) + f (x₀; x₁)(х – х₀) + … + f (x₀; x₁;…; x_n)(х – x₀)(х – x₁) … (х – х_n-1).

Оскільки за таблицею f (x₀) = 0,434966, f (x₀; x₁) = 0,926146, f (x₀; x₁; x₂) = – 0,2472, f (x₀; x₁; x₂; x₃) = – 0,14442, f (x₀; x₁; x₂; x₃; x₄) = 0,021447, f (x₀; x₁; x₂; x₃; x₄; х₅) = 0,007165, то інтерполяційна формула Ньютона набуває вигляду:

f (x) ≈ 0,434966 + 0,926146(х – 0,45) – 0,2472(х – 0,45)(х – 0,32) – 0,14442(х – 0,45)(х – 0,32) (х – 0,79) + 0,021447(х – 0,45)(х – 0,32)(х – 0,79)(х – 0,51) + 0,007165(х – 0,45)(х – 0,32)(х – 0,79)(х – 0,51)(х – 0,64). Задачу розв’язано.

Дата добавления: 2014-10-31