Тема: інтерполювання за схемою Ейткіна

Лабораторна робота 11.

(2г.)

Мета: Отримати відомості про метод інтерполювання за схемою Ейткіна та

навчитися застосовувати цей метод до конкретних задач.

Теоретичні відомості.

Якщо значення інтерполяційного многочлена треба обчислити лише в одній заданій точці, то немає потреби будувати самий многочлен. Звичайно для розв’язання такої задачі застосовують наступну інтерполяційну схему Ейткіна.

Нехай функцію f (x), яка в точках x_i набуває значень у_i = f (x_i) (і = 0, 1, …, n) задано таблично. Треба обчислити її значення в точці х є [x₀; x_n], яка не збігається з вузлами інтерполяції x_i. Нехай L_{(k,k+1,…,i)}(x) – це інтерполяційний многочлен з вузлами інтерполяції x_k, x_k+1,…, x_i, зокрема L_(k)(x) = f (x_k). Має місце рівність

L_{(k,k+1,…,i+1)}(x) = (1).

Схема Ейткіна обчислення значення L_n(x) = L_(0,1,…,n)(x) полягає у послідовних підрахунках за допомогою попередньої формули елементів наступної таблиці значень інтерполяційного многочлена.

L(0)(x)	L(0,1)(x)	L(0,1,2)(x)	…	L(0,1,…,n)(x)
L(1)(x)	L(1,2)(x)	…	…
L(2)(x)	…	…	…
…	…	…
L(n-1)(x)	L(n-1,n)(x)
L(n)(x)

Оцінка похибки значення L_n(x) заснована на формулі

R_n(f, x) = f (x) – L_n(x) ≈ L_n+1(x) – L_n(x).

Згідно цієї формули величину ε_m = L_m+1(x) – L_m(x) можна розглядати, як наближену оцінку похибки R_m(f, x) інтерполяційної формули f (x) ≈ L_m(x).

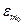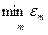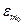Алгоритм методу: занумеруємо вузли інтерполяції x_i в порядку зростання │x_i – х│. Послідовно підраховуємо L₀(x), L₁(x), ε₀, L₂(x), ε₁, …. Якщо при деякому m ε_m ≤ Е, де Е – точність, яка нас задовольняє, то підрахунки закінчуються і вважають, що f (x) ≈ L_m(x). Якщо нерівність ε_m ≤ Е не виконується при жодному m, то знаходять = і вважають, що f (x) ≈ з оцінкою похибки . Оскільки значення │x_i – х│ послідовно зростають, то і ε_m, починаючи з деякого m можуть мати сталу тенденцію до зростання. Якщо так сталося, то з такого m підрахунки L_m(x) і ε_m припиняють.

Хід роботи.

Задача 1. За схемою Ейткіна обчислити значення функції e^2,72 з табличною точністю (тобто 6 вірних значущих цифр), якщо функція задана наступною таблицею.

2. Обчислити це значення з точністю 10 вірних значущих цифр.

і
xi	1,85	2,09	2,15	2,44	2,63	2,75	2,89	3,12
yi	6,35982	8,08491	8,58486	11,4730	13,8738	15,6426	17,9933	22,6464

Розв’язання. Спочатку згідно з цією схемою перенумеруємо вузли інтерполяції x_i в порядку зростання │х – x_i│, де х = 2,72:

i
xi	2,75	2,63	2,89	2,44	3,12	2,15	2,09	1,85
yi	15,6426	13,8738	17,9933	11,4730	22,6464	8,58486	8,08491	6,35982
х – xi	– 0,03	0,09	– 0,17	0,28	– 0,4	0,57	0,63	0,87

Побудуємо електронну таблицю для підрахунків за схемою Ейткіна (схожу на таблицю, яка була використана в лабораторній роботі 9). Надамо чарункам таких значень:

	A	B	C	D
	х0	– 0,03	15,6426	= (C2*B1 – C1*B2)/(B1 – B2)
	х1	0,09	13,8738
	х2	– 0,17	17,99331
…	…	…	…
	х7	0,87	6,35982
			ε =	= D1 – C1

Тут у стовпці В значення х – x_i, у стовпці С відповідні значення y_i = 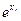= f (x_i) = L_(i)(x). У чарунці D1 формула визначає L₁(х) = L_(0,1)(х) згідно з формулою (1). У чарунці D9 обчислюємо похибку ε₀ = L₁(x) – L₀(x). В результаті дістанемо:

	A	B	C	D
	x0	-0,03	15,6426	15,20041
	x1	0,09	13,8738
	x2	-0,17	17,9933
	x3	0,28	11,4730
	x4	-0,4	22,6464
	x5	0,57	8,58486
	x6	0,63	8,08491
	x7	0,87	6,35982
			ε =	-0,44221

Оскільки ε₀ = – 0,4422155, то отримане значення L₁(2,72) = 15,20041 має тільки 2 вірні значущі цифри замість 6 потрібних. Тому зробимо другий крок схеми Ейткіна, як указано у наступній таблиці:

	A	B	C	D	E
	х0	– 0,03	15,6426	= (C2*B1 – C1*B2)/(B1 – B2)	= (D2*B1 – D1*B3)/(B1 – B3)
	х1	0,09	13,8738	↓
	х2	– 0,17	17,99331	↓
…	…	…	…	↓
	х7	0,87	6,35982
			ε =	= D1 – C1	→

А саме: 1) підрахуємо значення всіх многочленів другого степеня L_(k,k+1)(x) при х = 2,72, просто скопіювавши формулу з D1 у діапазон D2:D7; 2) у чарунку E1 запишемо формулу для підрахунку L₂(х) = L_(0,1,2)(х) згідно з формулою (1); 3) знайдемо у чарунці Е9 похибку ε₁, просто скопіювавши формулу з D9. В результаті дістанемо:

	A	B	C	D	E
	x0	-0,03	15,64263	15,20042	15,17913
	x1	0,09	13,87377	15,29976
	x2	-0,17	17,99331	15,5301
	x3	0,28	11,47304	16,07383
	x4	-0,4	22,64638	16,84781
	x5	0,57	8,584858	13,33432
	x6	0,63	8,084915	12,61329
	x7	0,87	6,35982
			ε =	-0,44222	-0,02128

Як бачимо, отримане значення L₂(2,72) = 15,17913 має лише 3 вірні значущі цифри. Отже, потрібним є третій крок схеми:

1) скопіюємо з Е1 у діапазон Е2:Е6, підрахувавши тим самим значення всіх многочленів третього степеня L_(k,k+1,k+2)(x) при х = 2,72;

2) у чарунку F1 запишемо формулу для підрахунку L₃(х) = L_(0,1,2,3)(х) згідно з (1);

3) скопіюємо формулу з Е9 у F9, тим самим підрахувавши похибку ε₂.

	A	B	C	D	E	F
	х0	– 0,03	15,6426	15,2004	15,17913	= (E2*$B1 – E1*$B4)/($B1 – $B4)
	х1	0,09	13,8738	15,2997	↓
	х2	– 0,17	17,99331	15,5301	↓
…	…	…	…	…
	х7	0,87	6,35982
			ε =	-0,44222	→	→

В результаті дістанемо:

	A	B	C	D	E	F
	x0	-0,03	15,64263	15,20042	15,17913	15,18024
	x1	0,09	13,87377	15,29976	15,19066
	x2	-0,17	17,99331	15,5301	15,12821
	x3	0,28	11,47304	16,07383	15,32653
	x4	-0,4	22,64638	16,84781	15,48335
	x5	0,57	8,584858	13,33432	14,70427
	x6	0,63	8,084915	12,61329
	x7	0,87	6,35982
			ε =	-0,44222	-0,02128	0,001116

Тут L₃(х) = 15,18024 уже має 4 вірні значущі цифри, потрібен ще крок.

Зазначимо, що формула у чарунку F1 була введена дещо по – іншому: адреса стовпця В тут є абсолютною. Якщо тепер скопіювати цю формулу у G1, то за правилами копіювання у Excel дістанемо G1 = (F2*$B4 – F1*$B2)/($B1 – $B4). Насправді ж згідно з (1) формула для підрахунку L₄(х) = L_(0,1,2,3,4)(х) виглядає так: G1 = (F2*$B5 – F1*$B2)/($B1 – $B5). Отже, достатньо для отримання правильної формули після копіювання виділити чарунку G1, підвести курсор у рядок формул Excel і виправити у відповідній формулі 4 на 5. Решта дій на четвертому кроці та ж сама:

	A	B	C	D	E	F	G
	х0	– 0,03	15,6426	15,2004	15,17913	15,17913	→ і виправити 4 на 5
	х1	0,09	13,8738	15,2997	15,19066	↓
	х2	– 0,17	17,9933	15,5301	15,12821	↓
…	…	…	…	…	…
	х7	0,87	6,35982
			ε =	– 0,44222	– 0,02128	0,001116	→

В результаті отримаємо:

	A	B	C	D	E	F	G
	x0	-0,03	15,64263	15,20042	15,17913	15,18024	15,18033
	x1	0,09	13,87377	15,29976	15,19066	15,17919
	x2	-0,17	17,99331	15,5301	15,12821	15,17377
	x3	0,28	11,47304	16,07383	15,32653	15,20107
	x4	-0,4	22,64638	16,84781	15,48335	15,23797
	x5	0,57	8,584858	13,33432	14,70427
	x6	0,63	8,084915	12,61329
	x7	0,87	6,35982
			ε =	-0,44222	-0,02128	0,001116	8,55E-05

Отримане значення L₄(х) = 15,18033 тепер має 6 вірних значущих цифр, що відповідає точності табличних даних. Отже, це відповідь на перше питання.

Для обчислення f (2,72) = e^2,72 з точністю 10^-10 необхідні ще кроки, які ми проведемо так само, як і попередній:

	A	B	C	D	E	F	G	H
	х0	– 0,03	15,6426	15,2004	15,17913	15,17913	15,2379	→
	х1	0,09	13,8738	15,2997	15,19066	15,17919	↓
	х2	– 0,17	17,9933	15,5301	15,12821	15,17377	↓
…	…	…	…	…	…
	х7	0,87	6,35982
			ε =	– 0,44222	– 0,02128	0,001116	8,55E-05	→

У чарунці H1 треба після копіювання виправити у відповідній формулі 5 на 6. В результаті

	A	B	C	D	E	F	G	H
	x0	-0,03	15,64263	15,20042	15,17913	15,18024	15,18033	15,18032
	x1	0,09	13,87377	15,29976	15,19066	15,17919	15,18021
	x2	-0,17	17,99331	15,5301	15,12821	15,17377	15,17957
	x3	0,28	11,47304	16,07383	15,32653	15,20107	15,18356
	x4	-0,4	22,64638	16,84781	15,48335	15,23797
	x5	0,57	8,584858	13,33432	14,70427
	x6	0,63	8,084915	12,61329
	x7	0,87	6,35982
			ε =	-0,44222	-0,02128	0,001116	8,55E-05	-6,2E-06

Значення L₅(х) = 15,18032 уже має 7 вірних значущих цифр. Максимально можна ще зробити 2 кроки так само, як попередні, і отримати значення L₇(х):

	A	B	C	D	E	F	G	H	I	J
	x0	-0,03	15,64263	15,20042	15,17913	15,18024	15,18033	15,18032	15,18032	15,18032
	x1	0,09	13,87377	15,29976	15,19066	15,17919	15,18021	15,18031	15,18032
	x2	-0,17	17,99331	15,5301	15,12821	15,17377	15,17957	15,18022
	x3	0,28	11,47304	16,07383	15,32653	15,20107	15,18356
	x4	-0,4	22,64638	16,84781	15,48335	15,23797
	x5	0,57	8,584858	13,33432	14,70427
	x6	0,63	8,084915	12,61329
	x7	0,87	6,35982
			ε =	-0,44222	-0,02128	0,001116	8,55E-05	-6,2E-06	-5,4E-07	-4,5E-08

Отже, значення L₇(х) має 9 вірних значущих цифр. Щоби їх побачити треба розсунути стовпець J, тоді маємо L₇(х) ≈ 15,1803222. Досягти 10 вірних значущих цифр принципово не можливо при даних задачі. Тому за схемою Ейткіна вважаємо, що e^2,72 ≈ 15,1803222 з оцінкою похибки ε₆ = 4,5E-08. Задачу закінчено.

Дата добавления: 2014-10-31