Тема: скінчені різниці, інтерполяційні формули Ньютона для рівновіддалених вузлів

Лабораторна робота 12.

(2г.)

Мета: Отримати відомості про скінчені різниці, про методи інтерполювання функцій

за інтерполяційними формулами Ньютона для рівновіддалених вузлів та

навчитися застосовувати ці методи до конкретних задач.

Теоретичні відомості.

Якщо вузли інтерполяції рівновіддалені: х₀, х₁ = х₀ + h, х₂ = х₀ + 2h, …, х_n = х₀ + nh, то інтерполяційна формула Ньютона спрощується, а алгоритми стають ефективнішими. Замість поділених різниць у таких випадках використовують скінчені різниці.

Означення 1. Нехай функція у = f (x) задана в точках х_k = х₀ + kh, де h – дійсна стала, k = 0, 1,…, n, y_k = f (х_k). Тоді величини Δу_i = Δ f _i = f (х_i+1) – f (х_i) називають скінченими різницями першого порядку. Скінчені різниці другого порядку Δ²у_i – це різниці перших різниць, тобто Δ²у_i = Δ² f _i = Δ f _{i +1} – Δ f _i = f (х_i+2) – 2 f (х_i+1) + f (х_i). Різниці Δⁿу_i порядку n – це різниці різниць порядку n – 1: Δⁿу_i = Δⁿ f _i = Δ^{n-1 f} _{i +1} – Δ^{n-1 f} _i.

Зазначимо, що нижні індекси при Δⁿу_i завжди ті ж самі, що й у від’ємника Δ^{n-1 f} _i.

Означення 2. Якщо вузли інтерполяції х_k = х₀ + kh, де h – дійсна стала, k = 0,1,…,n, y_k = f (х_k), то таблицю

х						n
х0	y0	Δу0	Δ^2у0	Δ^3у0	…	Δ^nу0
х1	y1	Δу1	Δ^2у1	Δ^3у1	…
х2	y2	Δу2	Δ^2у2	Δ^3у2
	…	…	…
хn-2	yn-2	Δуn-2	Δ^2уn-2
хn-1	yn-1	Δуn-1
хn	yn

називають горизонтальною таблицею її скінчених різниць.

Теорема. Нехай вузли інтерполяції х_k = х₀ + kh, де h – дійсна стала, k = 0,1,…,n, y_k = f (х_k). Тоді інтерполяційна формула Ньютона з поділеними різницями набуває вигляду:

f (x) ≈ L_n(x) = y₀ + tΔу₀ + Δ²у₀ + … + 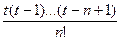Δⁿу₀, (1)

де t = (х – x₀)/h. Інтерполяційну формулу (1) називають першою інтерполяційною формулою Ньютона.

Насправді формулу (1) доцільно використовувати лише, якщо х міститься на початку таблиці, тобто х є [x₀; x₁]. Тому першу інтерполяційну формулу Ньютона називають також формулою Ньютона для інтерполювання вперед. Якщо х є [x₁; x₂], то недоцільно користуватись формулою (3) безпосередньо. У цьому разі за перший вузол треба взяти x₁ і в інтерполяційному многочлені використовувати скінчені різниці Δу₁, Δ²у₁, …, Δⁿу₁.

Якщо значення х лежить ближче до кінця відрізкаінтерполювання, то занумерувати вузли треба у зворотному порядку: x_n, x_n-1, …, x₁, x₀. Тоді інтерполяційна формула Ньютона з поділеними різницями набуває вигляду:

f (x) ≈ L_n(x) = y_n + tΔу_n-1 + 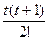Δ²у_n-2 + … + 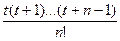Δⁿу₀, (2)

де t = (х – х_n)/h, її називають другою інтерполяційною формулою Ньютона або формулою Ньютона для інтерполювання назад.

Хід роботи.

Задача 1. Для функції f, заданої таблицею

i
xi		0,2	0,4	0,6	0,8
yi		0,1974	0,3805	0,5404	0,6747	0,7854

знайти її скінчені різниці Δ²у₃ , Δ⁴у₃, Δ⁵у₀ .

Розв’язання. Побудуємо таблицю скінчених різниць, звідки й отримаємо шукані значення. Надамо чарункам електронної таблиці таких значень:

	A	B	C	D	E	F	G
			= B3 – B2	→	→	→	→
		0,1974	↓	↓	↓	↓
		0,3805	↓	↓	↓
		0,5404	↓	↓
		0,6747	↓
		0,7854

У рядку 1 указані порядки скінчених різниць у відповідному стовпці. У стовпці B тут різниці порядку 0, тобто значення функції f у вузлі інтерполяції, номер якого вказаний у стовпці А. Правила копіювання Excel дозволяють отримати у відповідних чарунках саме ті формули, які повинні там бути згідно з означенням 2: так у чарунці Е4 міститься Δ³у₂. В результаті отримаємо таку трикутну таблицю:

	A	B	C	D	E	F	G
			0,1974	-0,01428	-0,00891	0,006519	-0,0022
		0,1974	0,183111	-0,0232	-0,00239	0,004321
		0,3805	0,159913	-0,02559	0,001927
		0,5404	0,134321	-0,02366
		0,6747	0,110657
		0,7854

Тут Δ³у₂ ≈ 0,0019, Δ⁵у₀ ≈ – 0,0022, скінчена різниця Δ⁴у₃ не визначена умовами задачі.

Задача 2. Для функції f, заданої таблицею

i
xi		0,2	0,4	0,6	0,8		1,2
yi		0,1974	0,3805	0,5404	0,6747	0,7854	0,8761

знайти наближені значення функції в точках x₁* = 0,1 і x₂* = 1,1.

Розв’язання. Побудуємо спочатку таблицю скінчених різниць, за якою знайдемо інтерполяційний многочлен Ньютона. Оскільки дана в умові таблиця відрізняється від таблиці в умові задачі 1 тільки доданим шостим вузлом інтерполяції, то і таблицю скінчених різниць цієї задачі можна отримати з такої таблиці попередньої задачі, просто продовживши її копіювання:

	A	B	C	D	E	F	G	H
			= B3 – B2	→	→	→	→	→
		0,1974	↓	↓	↓	↓	↓
		0,3805	↓	↓	↓	↓
		0,5404	↓	↓	↓
		0,6747	↓	↓
		0,7854	↓
		0,8761

В результаті отримаємо таку трикутну таблицю:

	A	B	C	D	E	F	G	H
			0,1974	-0,01428	-0,00891	0,006519	-0,0022	-0,00038
		0,1974	0,183111	-0,0232	-0,00239	0,004321	-0,00258
		0,3805	0,159913	-0,02559	0,001927	0,001739
		0,5404	0,134321	-0,02366	0,003667
		0,6747	0,110657	-0,02
		0,7854	0,09066
		0,8761

Оскільки в даному випадку x₁* = 0,1 міститься на початку таблиці, тобто x₁* є [x₀; x₁], то тут доцільно буде скористатися формулою Ньютона дляінтерполюваннявперед, тобто першою інтерполяційною формулою Ньютона (1). У ній задіяні тільки скінчені різниці Δ^kу₀, які всі містяться у рядку 2 останньої таблиці. За умовою t = (x₁* – x₀)/h = (0,1 – 0)/0,2 = 0,5. Побудуємо таблицю для підрахунків L_k(x₁*) (k = 1,…,6). Надамо таких значень чарункам електронної таблиці:

	A	B	C	D	E	F	G	H
	k
	t – k	0,5	= 0,5 – C11	→	→	→	→	→
	t*…*(t–k+1)		= B13*B12	→	→	→	→	→
	k!		= B14*C11	→	→	→	→	→
	uk(x1*)	= B2*B13/B14	→	→	→	→	→	→
	Lk(x1*)	= СУММ($B$15:B15)	→	→	→	→	→	→

Тут у рядку 11 позначений номер k одночлена u_k(x) = Δ^kу₀ першого інтерполяційного многочлена Ньютона L_k(x). У чарунці В12 значення кроку t = 0,5 вузлів інтерполяції. У рядку 13 підраховуються множники t(t – 1)(t – 2)…(t – k + 1) з номером k, позначеним у рядку 11. У рядку 14 підраховуються значення факторіалу k! з відповідним для цього стовпця номером k. У рядку 15 знаходимо значення одночлена u_k(x) з відповідним стовпцю номером k у заданій точці x₁*. Нарешті у рядку 16 послідовно знаходимо суми одночленів u_k(x₁*), шукане значення L₆(x₁*) дістанемо у чарунці H16.

В результаті отримаємо таку таблицю:

	A	B	C	D	E	F	G	H
	k
	t-k	0,5	-0,5	-1,5	-2,5	-3,5	-4,5	-5,5
	t*…*(t-k+1)		0,5	-0,25	0,375	-0,9375	3,28125	-14,7656
	k!
	uk(x1*)		0,098698	0,001786	-0,00056	-0,00025	-6E-05	7,89E-06
	Lk(x1*)		0,098698	0,100483	0,099926	0,099672	0,099612	0,099619

Отже, відповідь f (0,1) ≈ L₆(0,1) ≈ 0,099619. Щодо x₂* = 1,1, то це значення міститься ближче до кінця відрізкаінтерполювання, x₂* є [x₅; x₆]. Тож тут доцільно скористатися формулою Ньютона дляінтерполювання назад, тобто другою інтерполяційною формулою Ньютона (2). У ній задіяні тільки скінчені різниці Δ^kу_n-k (k = 1,…,n), які за означенням 2 всі містяться на діагоналі горизонтальної таблиці скінчених різниць. Оскільки зручніше для подальших підрахунків тримати всі ці значення на горизонталі, то таблицю скінчених різниць дещо переформуємо у порівнянні з означенням 2:

					n – 1	n
y0
y1	Δу0
y2	Δу1	Δ^2у0
…	…	…	…
yn-2	Δуn-3	Δ^2уn-4	Δ^3уn-5	…
yn-1	Δуn-2	Δ^2уn-3	Δ^3уn-4	…	Δ^n-1у0
yn	Δуn-1	Δ^2уn-2	Δ^3уn-3	…	Δ^n-1у1	Δ^nу0

Зауваження. Традиційно цю останню таблицю записують у такому форматі:

х	у	Δу	Δ^2у	Δ^3у	Δ^4у
х0	у0
		Δу0
х1	у1		Δ^2у0
		Δу1		Δ^3у0
х2	у2		Δ^2у1		Δ^4у0
		Δу3		Δ^3у1
х3	у3		Δ^2у2
		Δу4
х4	у4

Природно, що таку таблицю звичайно називають діагональною. Однак нам зручніше буде використовувати її для розрахунків у попередньому форматі. Отже, надамо чарункам електронної таблиці таких значень:

	A	B	C	D	E	F	G	H
		0,1974	↑
		0,3805	↑	↑
		0,5404	↑	↑	↑
		0,6747	↑	↑	↑	↑
		0,7854	↑	↑	↑	↑	↑
		0,8761	= В25 – В24	→	→	→	→	→

В результаті отримаємо ту ж саму таблицю скінчених різниць у новому форматі:

	A	B	C	D	E	F	G	H
	0,2	0,1974	0,197396
	0,4	0,3805	0,183111	-0,01428
	0,6	0,5404	0,159913	-0,0232	-0,00891
	0,8	0,6747	0,134321	-0,02559	-0,00239	0,006519
		0,7854	0,110657	-0,02366	0,001927	0,004321	-0,0022
	1,2	0,8761	0,09066	-0,02	0,003667	0,001739	-0,00258	-0,00038

Побудуємо таблицю для підрахунку L_k(x₂*). Тут за умовою t = (x₂* – x₆)/h =

(1,1 – 1,2)/0,2 = – 0,5. Надамо чарункам електронної таблиці таких значень:

	A	B	C	D	E	F	G	H
	k
	t + k	– 0,5	= – 0,5 + C27	→	→	→	→	→
	t*…*(t + k–1)		= B29*B28	→	→	→	→	→
	k!		= B30*C27	→	→	→	→	→
	uk(x2*)	= B25*B29/B30	→	→	→	→	→	→
	Lk(x2*)	= СУММ($B$32:B32)	→	→	→	→	→	→

Вона майже не відрізняється від копії таблиці для підрахунку L_k(x₁*) у нові чарунки: лише у чарунці В28 нове значення t = – 0,5, у формулі чарунки С28 заміняємо – на + і у чарунці В31 посилаємось на таблицю скінчених різниць у новому форматі. В результаті отримаємо таку таблицю:

	A	B	C	D	E	F	G	H
	k
	t+k	-0,5	0,5	1,5	2,5	3,5	4,5	5,5
	t*…(t+k-1)		-0,5	-0,25	-0,375	-0,9375	-3,28125	-14,7656
	k!
	uk(x2*)	0,876058	-0,04533	0,0025	-0,00023	-6,8E-05	7,06E-05	7,89E-06
	Lk(x2*)	0,876058	0,830728	0,833228	0,832999	0,832931	0,833001	0,833009

Шукане значення L₆(x₂*) у чарунці H32. Отже, відповідь f (1,1) ≈ L₆(1,1) ≈ 0,833.

Дата добавления: 2014-10-31