Примеры на вычисление пределов с пояснениями

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

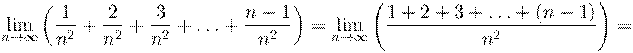
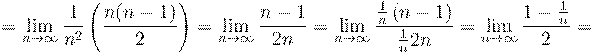
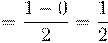
2. Вычислить предел числовой последовательности:

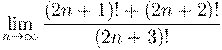
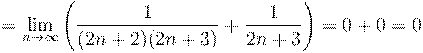
3. Вычислить предел числовой последовательности:

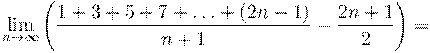
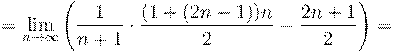
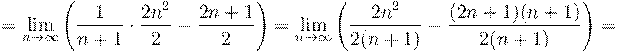
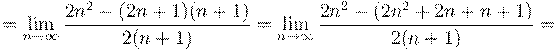
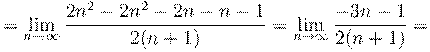
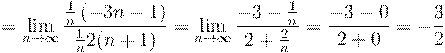
4. Вычислить предел числовой последовательности:

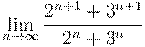
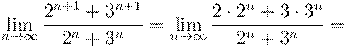
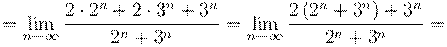
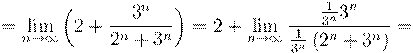
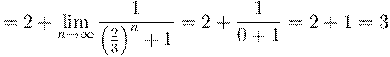
5. Вычислить предел числовой последовательности:

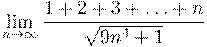
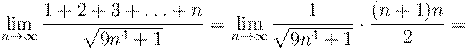
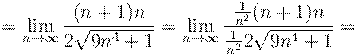
6. Вычислить предел числовой последовательности:

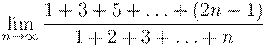
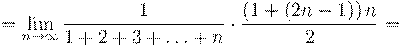
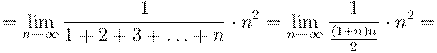
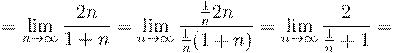
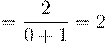
7. Вычислить предел числовой последовательности:

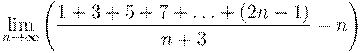
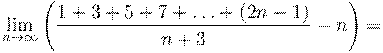
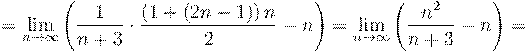
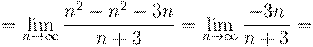
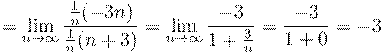
8. Вычислить предел числовой последовательности:

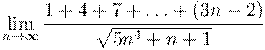
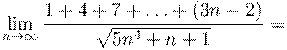
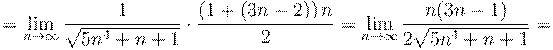
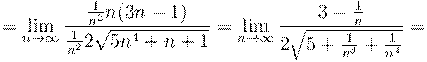
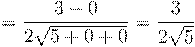
9. Вычислить предел числовой последовательности:

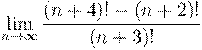
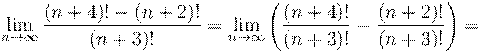
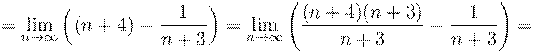
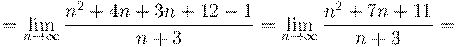
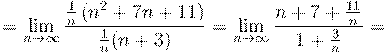
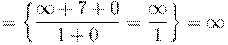
10. Вычислить предел числовой последовательности:

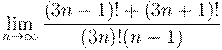
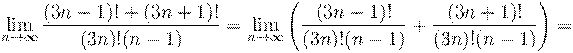
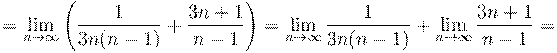
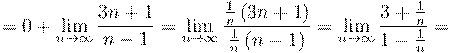
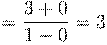
11. Вычислить предел числовой последовательности:

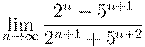
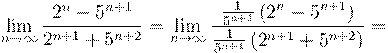
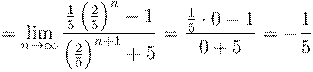
1)

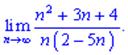
2)

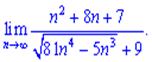
3)

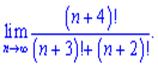
4)

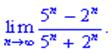
5)

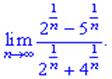
Решение.

1) Из числителя и знаменателя выделяем множитель, который вносит наибольший вклад и сокращаем на него

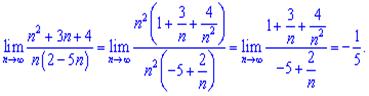
2) В такого типа примерах нужно вынести в знаменателе из-под корня множитель в наибольшей степени

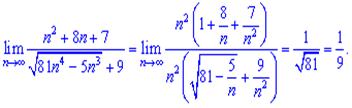
3) Надо раскладывать до наибольшего общего факториала

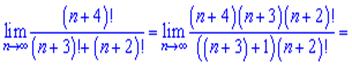
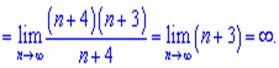
4) В данном примере 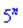растет значительно быстрее поэтому его выделяем как самый множитель

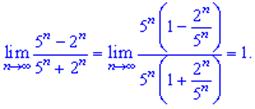
5) Величины и стремятся к нулю при . На основе этого вычисляем предел

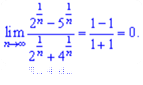
Решения большинства подобных примеров заключается в нахождении доминирующего множителя. Если он в числителе, то граница направляется к бесконечности, в знаменателе - к нулю. И только когда и там и там можно сократить на этот множитель дробь и получить предел в виде константы.

Задание:

1. Разобрать решения рассмотренных примеров

2. Вычислить следующие пределы:

1)

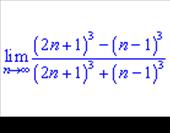
2)

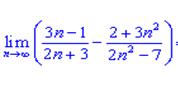
3) 4)

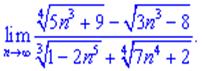
Раздел 2. Начала математического анализа

(Самостоятельная работа 48 час.)

2.1. Производная неявной функции (4 часа).

Пример 1. Найти производную 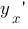неявной функции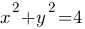

Решение. Так как у является функцией от х, то будем рассматривать y² как сложную функцию от х. Следовательно, . Продифференцировав по х обе части данного уравнения, получим, т.е.

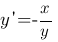
Пример 2. Найти производную 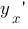неявной функции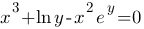

Решение. Дифференцируя по х обе части данного уравнения, получаем

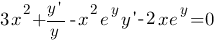т.е.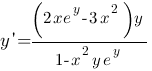

Пример 3. Найти производную 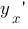неявной функции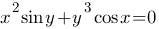

Решение. Дифференцируя по х обе части данного уравнения, получаем

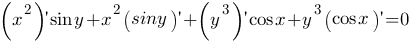
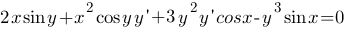
т.е.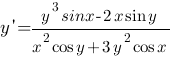

Пример 4. Найти производную 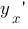неявной функции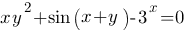

Решение. Дифференцируя по х обе части данного уравнения, получаем

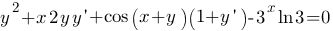
Раскроем скобки

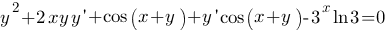
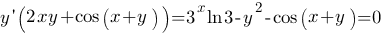
т.е.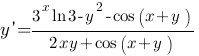

Задания.

1. Рассмотреть и разобрать рассмотренные решения примеров на данные темы.

2. Найти производные следующих неявных функций:

а) 3х² у² – 5х + sin y = 3y – 1;

б) 3х⁴ у⁵ + е^{7х – 4у} = 4х⁵ + 2у⁴ ;

в) у sin х = cos (х – у).

2.2. Исследование функции на экстремум с помощью второй производной (5 часа).

Правило нахождения экстремумов функции y = f(x) с помощью второй производной.

1. Найти производную f ’(x).

2. Найти стационарные точки данной функции, т.е. точки, в которых

f ’(x) = 0.

3. Найти вторую производную f ’’(x).

4. Исследовать знак второй производной в каждой из стационарных точек. Если при этом вторая производная окажется отрицательной, то функция в такой точке имеет максимум, а если положительной, то – минимум. Если же вторая производная равна нулю, то экстремум функции надо искать с помощью первой производной.

5. Вычислить значения функции в точках экстремума.

Пример. Исследовать на экстремум с помощью второй производной функцию: f(x) = x² – 2x - 3.
Решение: Находим производную: f ‘(x) = 2x - 2.
Решая уравнение f ’(x) = 0, получим стационарную точку х=1. Найдем теперь вторую производную: f ’’(x) = 2.
Так как вторая производная в) = x² – 2x - 3. стационарной точке положительна, f’’(1) = 2 > 0, то при x = 1 функция имеет минимум: f_min = f(1) = -4.
Ответ: Точка минимума имеет координаты (1; -4).

Задания.

1. Рассмотреть и разобрать рассмотренные решения примеров на данные темы.

2. Исследовать на экстремум с помощью второй производной функции:

а) f(x) = 1 – х⁴ ;

б) f(x) = х³ - 1;

в) f(x) = .

2.3. Приложение производной к решению физических задач (11 часов).

2.4. Составление кросснамберов по теме «Определенный интеграл»

(4 часа).

2.5 Вычисление объема тела и длины дуги кривой (12 часов)

Дата добавления: 2014-10-31