
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вычисление объема тела вращения
|
|
|
|
Объём тела, образованного вращением вокруг оси ох криволинейной трапеции, ограниченной непрерывной линией 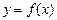 , отрезком оси абсцисс
, отрезком оси абсцисс 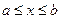 и прямыми
и прямыми 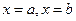 , вычисляется по формуле
, вычисляется по формуле
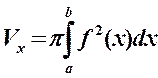 .
.
Объём тела, образованного вращением вокруг оси оу криволинейной трапеции, ограниченной непрерывной линией 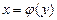 , отрезком оси ординат
, отрезком оси ординат 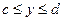 и прямыми
и прямыми 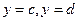 , вычисляется по формуле
, вычисляется по формуле
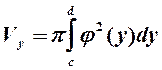 .
.
Пример 1. Вычислить объём тела, образованного вращением вокруг оси ох фигуры, ограниченной линиями 
Построим ограничивающие линии.
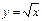 - ветвь параболы, расположенная выше оси OX, т.к.
- ветвь параболы, расположенная выше оси OX, т.к. 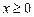 ;
;
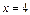 - прямая, параллельная оси OY;
- прямая, параллельная оси OY;
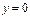 - ось OX.
- ось OX.

При вращении криволинейной трапеции (рис.11) вокруг оси ох образуется тело вращения.
Т. к. по условию криволинейная трапеция вращается вокруг оси ох, то объём тела вращения вычислим по формуле 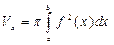 .
.
По условию 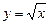 , т.е.
, т.е. 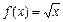 , тогда
, тогда 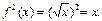 При этом
При этом 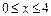 , т.е.
, т.е. 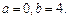
Тогда 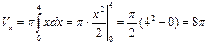 (ед3.)
(ед3.)
Пример 2. Вычислить объём тела, образованного вращением вокруг оси оу фигуры, ограниченной линиями 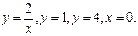
Построим ограничивающие линии.
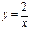 - гипербола, ветви которой расположены в I и III координатных углах;
- гипербола, ветви которой расположены в I и III координатных углах;
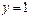 - прямая, параллельная оси OX;
- прямая, параллельная оси OX;
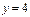 - прямая, параллельная оси OX;
- прямая, параллельная оси OX;
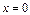 - ось OY.
- ось OY.
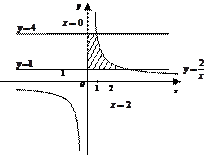
При вращении криволинейной трапеции (рис.12) вокруг оси оу образуется тело вращения.
Т.к. по условию криволинейная трапеция вращается вокруг оси оу, то объём тела вращения вычислим по формуле 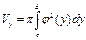 .
.
По условию 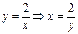 , т.е.
, т.е. 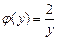 , тогда
, тогда 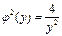 .
.
При этом 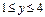 , т.е.
, т.е. 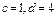 .
.
Тогда 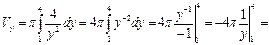
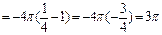 (ед3.)
(ед3.)
Пример 3. Вычислить объём тела, образованного вращением вокруг оси ох фигуры, ограниченной линиями 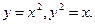
Построим ограничивающие линии.
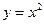 - парабола с вершиной в точке
- парабола с вершиной в точке 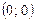 , симметрична относительно оси OY;
, симметрична относительно оси OY;
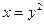 - парабола с вершиной в точке
- парабола с вершиной в точке 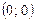 , симметрична относительно оси OX.
, симметрична относительно оси OX.
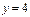 - прямая, параллельная оси OX;
- прямая, параллельная оси OX;
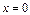 - ось OY.
- ось OY.
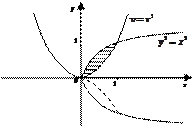
Рис. 13.
При вращении криволинейной трапеции (рис.13) вокруг оси OX образуется тело вращения.
По условию фигура вращается вокруг оси OX. Тогда искомый объём равен разности двух объёмов: объёма Vx1, полученного от вращения вокруг оси OX фигуры, ограниченной линиями 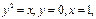 и объёма Vx2, полученного от вращения вокруг оси OX фигуры, ограниченной линиями
и объёма Vx2, полученного от вращения вокруг оси OX фигуры, ограниченной линиями 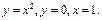 Т.о.
Т.о. 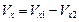
Вычислим 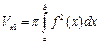 .
.
Для Vx1: 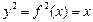 , при этом
, при этом 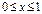 . Тогда
. Тогда
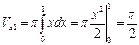 (ед3.)
(ед3.)
Вычислим 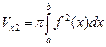 .
.
Для Vx2: 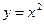 ,т. е
,т. е 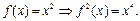 Тогда
Тогда 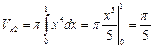 (ед3.)
(ед3.)
Т.о. 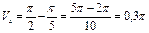 (ед3.)
(ед3.)
Задания для самостоятельной работы по теме "Вычисление объема тела вращения"
1. Вычислить объём тела, образованного вращением вокруг оси ох фигуры, ограниченной линиями: 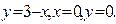
2. Вычислить объём тела, образованного вращением вокруг оси ох фигуры, ограниченной линиями: 
3. Вычислить объём тела, образованного вращением вокруг оси ох фигуры, ограниченной линиями: 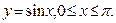
4. Вычислить объём тела, образованного вращением вокруг оси ох фигуры, ограниченной линиями: 
5. Вычислить объём тела, образованного вращением вокруг оси ох фигуры, ограниченной линиями: 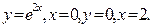
6. Вычислить объём тела, образованного вращением вокруг оси оу фигуры, ограниченной линиями: 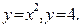
7. Вычислить объём тела, образованного вращением вокруг оси оу фигуры, ограниченной линиями: 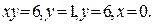
8. Вычислить объём тела, образованного вращением вокруг оси оу фигуры, ограниченной линиями: 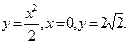
9. Вычислить объём тела, образованного вращением вокруг оси оу фигуры, ограниченной линиями: 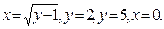
10. Вычислить объём тела, образованного вращением вокруг оси оу фигуры, ограниченной линиями: 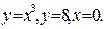
Ответы для самостоятельной работы по теме "Вычисление объема тела вращения"
1. 9π ед3
2. 18π ед3
3. 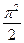 ед3
ед3
4. 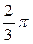 ед3
ед3
5. 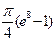 ед3
ед3
6. 8π ед3
7. 30π ед3
8. 8π ед3
9. 7,5 ед3
10. 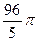 ед3
ед3
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 9695; Нарушение авторских прав?; Мы поможем в написании вашей работы!