Нахождение длины дуги кривой, если линия задана в полярной системе координат

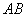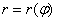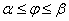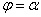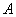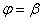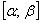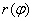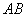Пусть кривая задана в полярных координатах уравнением , где , и при этом значение определяет точку , а значение – точку . Если на промежутке функция имеет непрерывную производную , то длина кривой выражается следующей формулой:

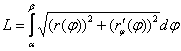
Пример 6. Вычислить длину дуги кривой, заданную в полярной системе координат
,

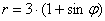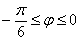
Решение. Используем формулу .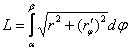

Найдём производную по «фи»:

Составим и максимально упростим подкоренное выражение:

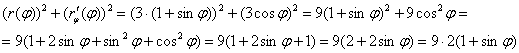
Заливаем топливо:

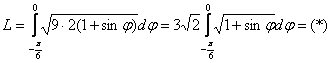
Используем формулу двойного угла 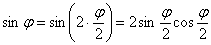и основное тригонометрическое тождество :

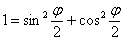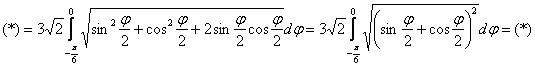
Теперь нужно разобраться с функцией 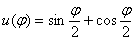на отрезке 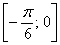, чтобы правильно избавиться от корня. Мысленно представив график, видно, что функция здесь положительна, но это очевидно далеко не всем, и в этой ситуации можно использовать нечто похожее на метод интервалов. Вычислим значение функции в какой-нибудь промежуточной точке, например, посерединке в точке :

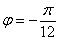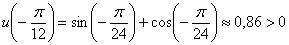, а значит, 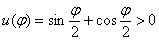и в любой точке интервала 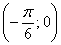. К слову, и на концах тоже.

Ответ:

Пример 7. Вычислить длину дуги кривой, заданную в полярной системе координат
,

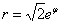Решение. Используем формулу:

Ответ: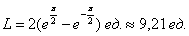

Задания для самостоятельной работы по теме "Вычисление длины дуги кривой"

1. Найти длину дуги кривой y = ln x, .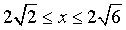

2. Вычислить длину дуги полукубической параболы y = x ^3/2 от х = 0 до х = 5.

3. Вычислить длины дуг кривых, заданных уравнениями в прямоугольной системе координат: , .

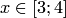4. Найти длину первого витка спирали Архимеда r = φ.

5. Найти длину одной арки циклоиды

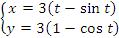
6.Вычислить длину дуги кривой, заданной уравнением в полярных координатах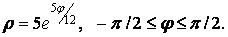

7. Вычислить длину дуги кривой: 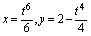, между точками пересечения с осями координат.

Ответы для самостоятельной работы по теме "Вычисление длины дуги кривой"

1. .

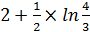2. .

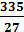3. .

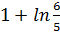4.

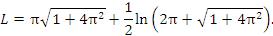
5.

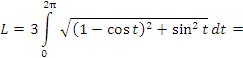
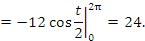
6. .

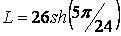7. .

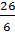2.6. Применение определенного интеграла к решению физических и технических задач (12 часов)

Применение определенного интеграла к решению физических и технических задач

Определенный интеграл помогает решать ряд физических и общетехнических задач, поэтому знания, полученные вами на этом уроке, помогут в вашей дальнейшей учебе и практической деятельности.

Задача о вычислении пути

Согласно физическому смыслу первой производной, производная функции в точке есть мгновенная скорость точки, т.е. 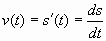. Отсюда, 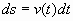. Интегрируя полученное равенство в пределах от t₁ до t₂ получаем

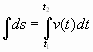
Тогда путь, пройденный точкой при неравномерном движении по прямой с переменной скоростью 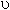(е) за отрезок времени [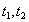]выражается интегралом

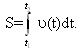(1)

Пример 1. Скорость прямолинейного движения тела выражается формулой 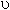= 2t+3t²(м/с). Найти путь, пройденный телом за 5 секунд от начала движения.

Решение.

Пример 2. Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью v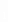=(6t²+2t) м/с, второе – со скоростью v²=(4t+5) м/с. На каком расстояния друг от друга они окажутся через 5 с?

Решение. Искомая величина есть разность расстояний, пройденных телами за 5 с.

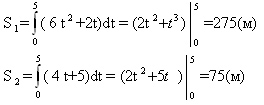
Таким образом, S=S₁-S₂= 275-75=200 (м).

Задача о вычислении работы переменной силы

Пусть материальная точка под действием силы F движется по прямой. Если действующая сила постоянна, а пройденный путь равен s, то как известно из курса физики, работа А этой F вычисляется по формуле:

А= F*s

Работу переменной силы f(x) при перемещении по оси Оx материальной точки от x=a до x=b, находим по формуле (2):

A=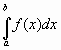 (2)

Решении задач на вычисление работы силы упругости, связанных с растяжением и сжатием пружин, основывается на законе Гука. По закону Гука сила F, растягивающая или сжимающая пружину, пропорциональная этому растяжению или сжатию, т.е. F=kx, где x – величина растяжения или сжатия, k – коэффициент пропорциональности.

Пример 1. Сила упругости F пружины, растянутой на 1¹ = 0,05 м, равна 3H. Какую работу надо произвести, чтобы растянуть пружину на 1₂ =0,1 м?

Решение. Подставив данные в формулу закона Гука, получим: 3=k*0.05, т.е. k=60, следовательно, сила упругости выражается соотношением F=60x. Найдем работу переменной силы по формуле (2), полагая, что а=0; b=0,1:

A=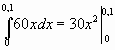=0,3Дж

Задача о силе давления жидкости

Согласно закону Паскаля величина P давления жидкости на горизонтальную площадку вычисляется по формуле P=gphS, (3)

Где g – ускорение свободного падения в м/с²;

p– плотность жидкости в кг/м³;

h – глубина погружения площадки в м;

S – площадь площадки в м².

По этой формуле нельзя искать давление жидкости на вертикально погруженную пластинку, так как ее разные точки лежат на разных глубинах.

Пусть в жидкость погружена вертикально пластина, ограниченная линиями х = а, х = b, у1 = f 1(x) и у2= f 2(х); система координат выбрана так, как указано на рисунке 1.

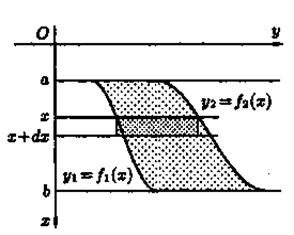
рисунок 1

Для решения задачи разобьем пластину на n частей (малых горизонт альных полосок) прямыми, параллельными поверхности жидкости (т.е. параллельными оси OY). На глубине х выделим одну из них и обозначим через f(x) ее длину, а через 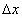ее ширину. Приняв полоску за прямоугольник, находим ее площадь .

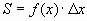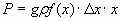
Найдем дифференциал dp этой функции.

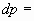
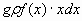
Тогда по закону Паскаля интегрируя полученное равенство в пределах от х = а до х = b, получим

P=g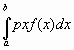 (4)

Пример 1. Аквариум имеет форму прямоугольного параллелепипеда. Найдем силу давления воды (плотность воды 1000 кг/м³), наполняющей аквариум, на одну из его вертикальных стенок, размеры которой 0,4 м x 0,7 м.

Решение. Выберем систему координат так, чтобы оси Оy и Оx соответственно содержали верхнее основание и боковую сторону вертикальной стенки аквариума. Для нахождения силы давления воды на стенку воспользуемся формулой (3). Стенка имеет форму прямоугольника, поэтому 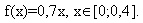Так как пределы интегрирования а=0 и b=0,4, то получим:

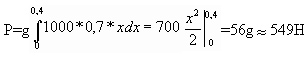
Дата добавления: 2014-10-31