
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства функций непрерывных в точке. Арифметические свойства непрерывных функций
|
|
|
|
Непрерывность функции, геометрический смысл, критерий непрерывности.
Ответ:Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения.Свойства[править | править вики-текст]
Локальные [править | править вики-текст]
- Функция, непрерывная в точке a, является ограниченной в некоторой окрестности этой точки.
- Если функция f непрерывна в точке a и f (a)>0 (или f (a)<0), то f (x)>0 (или f (x)<0) для всех x, достаточно близких к a.
- Если функции f и g непрерывны в точке a, то функции f + g и f ⋅ g тоже непрерывны в точке a.
- Если функции f и g непрерывны в точке a и при этом g (a)≠0, то функция f / g тоже непрерывна в точке a.
- Если функция f непрерывна в точке a и функция g непрерывна в точке b = f (a), то их композиция h = g ∘ f непрерывна в точке a.
Глобальные [править | править вики-текст]
- Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
- Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
- Областью значений функции f, непрерывной на отрезке [ a, b ], является отрезок [min f, max f ], где минимум и максимум берутся по отрезку [ a, b ].
- Если функция f непрерывна на отрезке [ a, b ] и f (a)⋅ f (b)<0, то существует точка ξ ∈(a, b), в которой f (ξ)=0.
- Если функция f непрерывна на отрезке [ a, b ] и число φ удовлетворяет неравенству f (a)< φ < f (b) или неравенству f (a)> φ > f (b), то существует точка ξ ∈(a, b), в которой f (ξ)= φ.
- Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
- Монотонная функция на отрезке [ a, b ] непрерывна в том и только в том случае, когда область ее значений является отрезком с концами f (a) и f (b).
- Если функции f и g непрерывны на отрезке [ a, b ], причем f (a)< g (a) и f (b)> g (b), то существует точка ξ ∈(a, b), в которой f (ξ)= g (ξ). Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.
Ответ: Свойства функций, непрерывных в точке
Поскольку точки  непрерывности функции
непрерывности функции  задаются условием
задаются условием  , то часть свойств функций, непрерывных в точке
, то часть свойств функций, непрерывных в точке  , следует непосредственно из свойств пределов. Сформулируем их в виде следующей теоремы.
, следует непосредственно из свойств пределов. Сформулируем их в виде следующей теоремы.
Теорема 3.1 Пусть функции  и
и 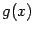 непрерывны в точке
непрерывны в точке  . Тогда функции
. Тогда функции 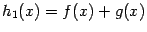 ,
,  ,
,  непрерывны в точке
непрерывны в точке  . Если
. Если 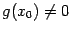 , то функция
, то функция  также непрерывна в точке
также непрерывна в точке  .
.
Доказательство. Оно сразу же следует из теорем о пределах 2.8, 2.9, 2.10 и следствия 2.5.
Как непосредственное следствие этой теоремы получается следующее
Предложение 3.3 Рассмотрим множество всех функций, определённых в некоторой фиксированной окрестности  точки
точки  и непрерывных в этой точке. Тогда это множество
и непрерывных в этой точке. Тогда это множество 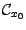 является линейным пространством, то есть замкнуто относительно сложения и умножения на постоянные:
является линейным пространством, то есть замкнуто относительно сложения и умножения на постоянные:

Доказательство. Действительно, постоянные  и
и  -- это непpеpывные функции (в любой точке); по пpедыдущей теоpеме тогда непpеpывны в точке
-- это непpеpывные функции (в любой точке); по пpедыдущей теоpеме тогда непpеpывны в точке  пpоизведения
пpоизведения 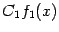 и
и  . Но тогда по этой же теоpеме непpеpывна в точке
. Но тогда по этой же теоpеме непpеpывна в точке  и сумма
и сумма  .
.
Теорема 3.2 Пусть функции  и
и 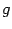 таковы, что существует композиция
таковы, что существует композиция  ,
,  . Пусть функция
. Пусть функция 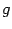 непрерывна в точке
непрерывна в точке  , а функция
, а функция  непрерывна в соответствующей точке
непрерывна в соответствующей точке 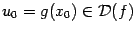 . Тогда композиция
. Тогда композиция  непрерывна в точке
непрерывна в точке  .
.
Доказательство. Заметим, что равенство 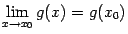 означает, что при
означает, что при 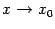 будет
будет  . Значит,
. Значит,

(последнее равенство следует из непрерывности функции  в точке
в точке  ). Значит,
). Значит,
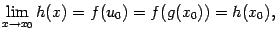
а это равенство означает, что композиция  непрерывна в точке
непрерывна в точке  .
.
Заметим, что, очевидно, в предыдущих двух теоремах можно было бы заменить базу 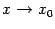 на односторонние базы
на односторонние базы  или
или  и получить аналогичные утверждения для непрерывности слева или справа:
и получить аналогичные утверждения для непрерывности слева или справа:
Теорема 3.3 Пусть функции  и
и 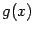 непрерывны слева (справа) в точке
непрерывны слева (справа) в точке  . Тогда функции
. Тогда функции 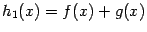 ,
,  ,
,  непрерывны слева (соотв. справа) в точке
непрерывны слева (соотв. справа) в точке  . Если
. Если 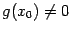 , то функция
, то функция  также непрерывна слева (спpава) в точке
также непрерывна слева (спpава) в точке  .
.
Теорема 3.4 Пусть функция 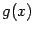 непрерывна слева (справа) в точке
непрерывна слева (справа) в точке  , а функция
, а функция 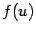 непрерывна в точке
непрерывна в точке  . Тогда композиция
. Тогда композиция  непрерывна слева (соотв. справа) в точке
непрерывна слева (соотв. справа) в точке  .
.
28.преход к пределу под знаком непрерывной функции. Непрерывность сложной и обратной функции.. непрерывность элементарных функций.
Ответ: Если lim f(x)=A, а функция g непрерывна в точке А, то lim g(f(x))=g(lim f(x)). Определение 1. Функция f(x) называется непрерывной в точке x0, если 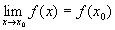 .
.
Дадим несколько расшифровок этого важнейшего определения.
а) Вспоминая понятие предела, запишем непрерывность f(x) в точке х0 в виде

б) Так как х0=lim x, то непрерывность в точке х0 можно записать в виде

Отсюда следует важнейшее свойство непрерывной функции: для непрерывной функции можно переставлять местами знак функции и знак предельного перехода
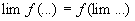
в) Обозначим Dx=x-x0 (приращение аргумента) и Df=f(x)-f(x0) (приращение функции). Тогда непрерывность в точке х0 означает, что  , т.е. бесконечно-малому приращению аргумента соответствует бесконечно-малое приращение функции.
, т.е. бесконечно-малому приращению аргумента соответствует бесконечно-малое приращение функции.
Введем обозначения:

если эти пределы существуют.
Определение 2. Функция f(x) называется непрерывной в точке х0 слева (справа) если f(x0)=f(x0 – 0) (f(x0)=f(x0+0)). Очевидно,что непрерывность в точке х0 означает непрерывность слева и справа одновременно.
Определение 3. Функция f(x) называется непрерывной на некотором множестве Х, если она непрерывна в каждой точке этого множества, т.е. если
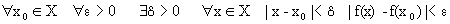
Обратите внимание, где стоит квантор , это важно.
, это важно.
Определение. Если функция f(x) не является непрерывной в точке х0, то говорят, что в точке х0 функция f(x) имеет разрыв.
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 3171; Нарушение авторских прав?; Мы поможем в написании вашей работы!