П. 4. Эллипсоид, гиперболоиды, параболоиды

а) эллипсоид

Каноническое уравнение 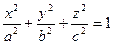(1)

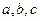- полуоси

Уравнение касательной плоскости в точке 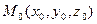эллипсоида (1):

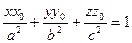
Уравнения плоскостей, которые пересекают эллипсоид (1) с условием 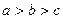по окружностям:

.

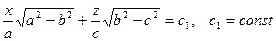
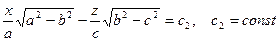Параметрические уравнения эллипсоида:

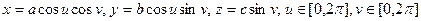
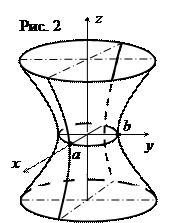
б) однополостный гиперболоид

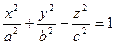(2)

Плоскость 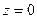пересекает однополостный гиперболоид по эллипсу , который называется горловым эллипсом.

Через каждую точку 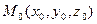горлового эллипса проходит прямолинейная образующая первого семейства

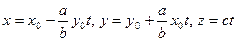
и прямолинейная образующая второго семейства

.

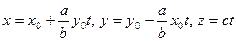Другие формы записи прямолинейных образующих, проходящих через точку горлового эллипса:

.

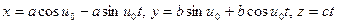
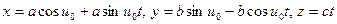Задание прямолинейных образующих как пересечение плоскостей

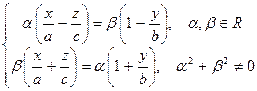- первое семейство

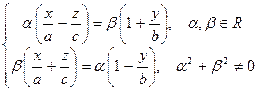- второе семейство.

Через каждую точку 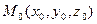однополостного гиперболоида (2) проходит по одной прямолинейной образующей каждого семейства, направляющие векторы 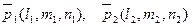которых определяются следующим образом:

,

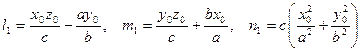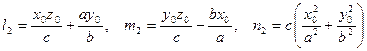
Две прямолинейные образующие различных семейств всегда лежат в одной плоскости и параллельны тогда и только тогда, когда они проходят через диаметрально противоположные точки горлового эллипса.

Две прямолинейные образующие одного семейства на однополостном гиперболоиде скрещиваются.

Уравнение касательной плоскости в точке 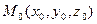гиперболоида (2):

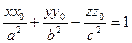
Уравнения плоскостей, которые пересекают гиперболоид (2) с условием 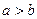по окружностям:

.

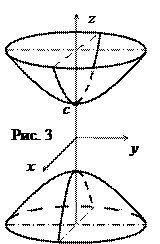
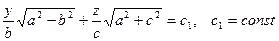
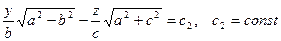Параметрические уравнения гиперболоида:

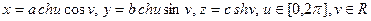
Параметризация однополостного гиперболоида

,

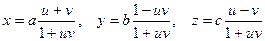в которой прямолинейные образующие являются координатными линиями.

Асимптотический конус двуполостного гиперболоида (2):

в) двуполостный гиперболоид:

Каноническое уравнение 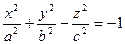(3)

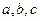- полуоси

Уравнение касательной плоскости в точке 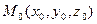гиперболоида (3):

.

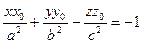Асимптотический конус двуполостного гиперболоида (3):

Параметрические уравнения двуполостного гиперболоида:

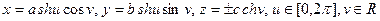
Уравнения плоскостей, которые пересекают гиперболоид (3) с условием 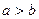по окружностям:

.

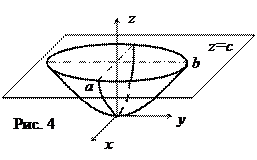
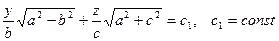
г) эллиптический параболоид

Каноническое уравнение 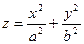(4)

Уравнение касательной плоскости в точке 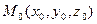эллиптического параболоида (4):

.

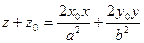Уравнения плоскостей, которые пересекают параболоид (4) с условием 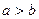по окружностям:

.

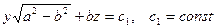
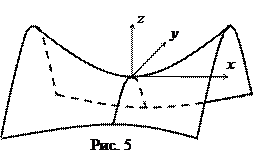
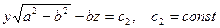д) гиперболический параболоид

Каноническое уравнение

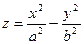(5)

Уравнение касательной плоскости в точке 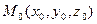гиперболического параболоида (5):

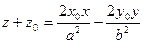
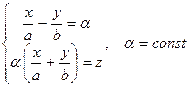
- первое семейство прямолинейных образующих

- второе семейство прямолинейных образующих.

Дата добавления: 2014-10-31