
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
МАТЕМАТИКА. Задания на контрольную работу №1
|
|
|
|
Задания на контрольную работу №1.
Задание №1. По координатам вершины пирамиды А1А2А3А4 найти:
1. длину ребра А 1 А 2; А 1 А 3;
2. угол между ребрами 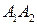 и
и  ;
;
3. площадь грани 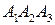 ;
;
4. объем пирамиды 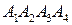 ;
;
5. уравнение прямых 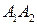 и
и  ;
;
6. уравнения плоскостей 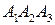 и
и 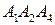 ;
;
7. угол между плоскостями 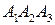 и
и 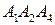 .
.
 , ,
|  , ,
| 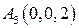 , ,
|  . .
| |
 , ,
|  , ,
|  , ,
| 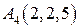 . .
| |
 , ,
|  , ,
| 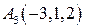 , ,
|  . .
| |
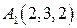 , ,
| 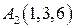 , ,
| 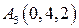 , ,
| 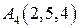 . .
| |
 , ,
|  , ,
| 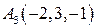 , ,
|  . .
| |
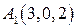 , ,
|  , ,
|  , ,
| 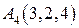 . .
| |
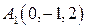 , ,
| 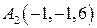 , ,
| 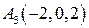 , ,
|  . .
| |
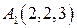 , ,
|  , ,
|  , ,
| 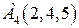 . .
| |
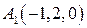 , ,
|  , ,
| 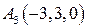 , ,
|  . .
| |
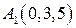 , ,
|  , ,
|  , ,
| 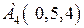 . .
|
Задание №2. Дана система трех линейных уравнений с тремя неизвестными. Требуется найти ее решение с помощью формул Крамера.
1. 
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 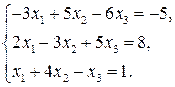
|
7. 
| 8. 
|
9. 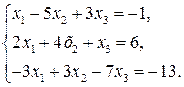
| 10. 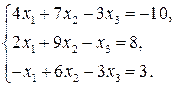
|
Задание №3. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1. а)  ; б)
; б) 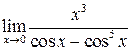 ;
;
в)  ; г)
; г)  .
.
2. а)  ; б)
; б) 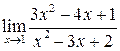 ;
;
в) 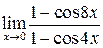 ; г)
; г)  .
.
3. а) 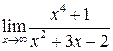 ; б)
; б)  ;
;
в)  ; г)
; г) 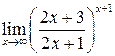 .
.
4. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 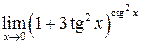 .
.
5. а) 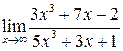 ; б)
; б) 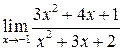 ;
;
в) 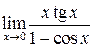 ; г)
; г) 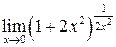 .
.
6. а)  ; б)
; б) 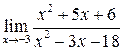 ;
;
в) 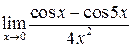 ; г)
; г)  .
.
7. а) 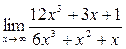 ; б)
; б) 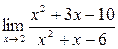 ;
;
в) 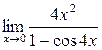 ; г)
; г) 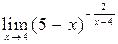 ;
;
8. а) 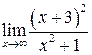 ; б)
; б)  ;
;
в) 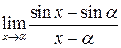 ; г)
; г) 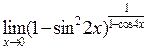 .
.
9. а) 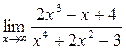 ; б)
; б)  ;
;
в) 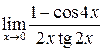 ; г)
; г) 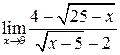 .
.
10. а)  ; б)
; б)  ;
;
в) 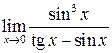 ; г)
; г)  .
.
Задание №4. Исследовать функцию 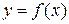 на непрерывность. Найти точки разрыва функции и определить их тип. Построить схематический график функции.
на непрерывность. Найти точки разрыва функции и определить их тип. Построить схематический график функции.
1. 
| 2. 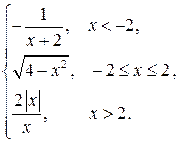
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 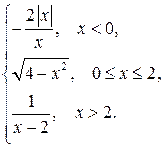
| 8. 
|
9. 
| 10. 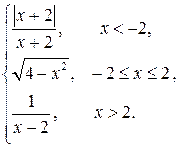
|
Задание №5. Найти производные первого порядка данных функций.
1. 1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4) 
2. 1) 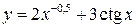 , 2)
, 2)  , 3)
, 3) 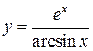 , 4)
, 4) 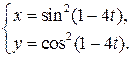
3. 1)  , 2)
, 2)  , 3)
, 3) 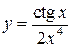 , 4)
, 4) 
4. 1) 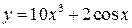 , 2)
, 2) 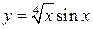 , 3)
, 3) 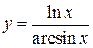 , 4)
, 4) 
5. 1)  , 2)
, 2)  , 3)
, 3) 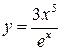 , 4)
, 4) 
6. 1) 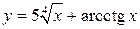 , 2)
, 2)  , 3)
, 3) 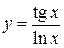 , 4)
, 4) 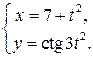 .
.
7. 1)  , 2)
, 2) 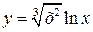 , 3)
, 3) 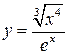 , 4)
, 4)  .
.
8. 1)  , 2)
, 2) 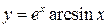 , 3)
, 3) 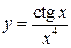 , 4)
, 4) 
9. 1) 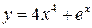 , 2)
, 2)  , 3)
, 3)  , 4)
, 4) 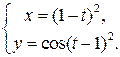
10. 1)  , 2)
, 2) 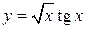 , 3)
, 3) 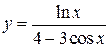 , 4)
, 4) 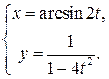 .
.
Задание №6. Составить уравнение касательной и нормали к кривой в точке с абсциссой 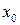 .
.
1. 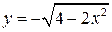 , , 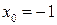 . .
| 2. 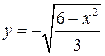 , , 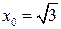 . .
|
3. 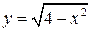 , , 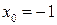 . .
| 4. 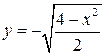 , , 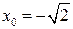 . .
|
5. 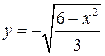 , , 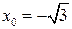 . .
| 6. 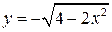 , , 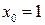 . .
|
7.  , , 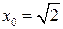 . .
| 8.  , , 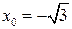 . .
|
9.  , , 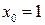 . .
| 10. 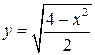 , ,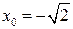 . .
|
Задание №7. Вычислить предел функции с помощью правила Лопиталя.
1. 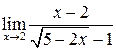 ; ;
| 2.  ; ;
|
3. 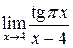 ; ;
| 4. 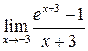 ; ;
|
5. 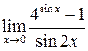 ; ;
| 6. 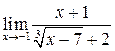 ; ;
|
7. 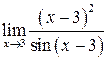 ; ;
| 8. 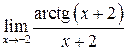 ; ;
|
9. 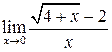 ; ;
| 10. 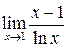 . .
|
Задание №8. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить график.
1.  ; ;
| 2. 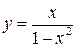 ; ;
|
3. 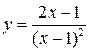 ; ;
| 4. 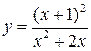 ; ;
|
5.  ; ;
| 6. 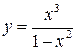 ; ;
|
7. 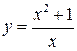 ; ;
| 8.  ; ;
|
9. 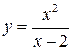 ; ;
| 10.  . .
|
Задание №9. Найти неопределенные интегралы. В пунктах а) и б) результаты проверить дифференцированием.
1. а)  ; ;
| б) 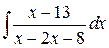 ; ;
| в)  . .
|
2. а)  ; ;
| б)  ; ;
| в) 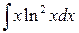 . .
|
3. а)  ; ;
| б) 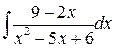 ; ;
| в)  . .
|
4. а)  ; ;
| б)  ; ;
| в)  . .
|
5. а)  ; ;
| б)  ; ;
| в)  . .
|
6. а) 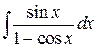 ; ;
| б)  ; ;
| в) 
|
7. а) 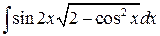 ; ;
| б) 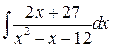 ; ;
| в) 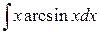 . .
|
8. а) 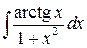 ; ;
| б)  ; ;
| в)  . .
|
9. а)  ; ;
| б) 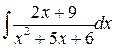 ; ;
| в)  . .
|
10. а)  ; ;
| б)  ; ;
| в) 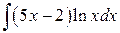 . .
|
Список рекомендуемой литературы
1. Пискунов Н.С. Дифференциальное и интегральное исчисления для ВТУЗов. Том 1. – М.: Интеграл-Пресс, 2004. – 416 с.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Часть I – М.:Образование, 2002г.
3. Шипачев В.С. Задачник по высшей математике: Учеб. пособие для вузов. – 2-е изд., испр. – М.: Высш.шк., 2001г. – 304 с.
4. Шипачев В.С. Высшая математика. Учеб. для вузов. – 5-е изд., стер. – М.: Высш.шк., 2002. – 479 с.
5. Клетеник Д.В. Сборник задач по аналитической геометрии. М.:Наука, 2002 г.
6. Барвин И.И. Высшая математика: Учеб. пособие для студентов вузов. – 3-е изд., стереотип. – М.: Академия, 2002. – 616 с.
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 629; Нарушение авторских прав?; Мы поможем в написании вашей работы!