Решение системы общего вида

Пусть задана система линейных уравнений общего вида (15.1), где т ≤ n, т.е. число неизвестных не меньше числа уравнений. Представим общий порядок решения этой системы.

1. Необходимо определить совместность системы, т.е. опре­делить сначала ранги матрицы системы А и расширенной мат­рицы A_B. По теореме Кронекера-Капелли если ранги этих матриц не совпадают, то система несовместна и тогда нет смысла ее решать. Если же ранги матриц А и А_B равны, то система (15.1) совместна.

Определение 1. Рангом совместной системы линейных алгеб­раических уравнений называется ранг ее матрицы.

2. Пусть система (15.1) совместна и ранг ее равен r. Вы­делим в матрице системы (15.2) некоторый базисный минор; предположим, что именно первые r строк матриц А и А_B яв­ляются базисными. Тогда по теореме о базисном миноре ос­тальные строки матрицы являются линейными комбинациями остальных строк. В свою очередь это означает, что в системе (15.1) первые r уравнений, соответствующие базисным стро­кам матрицы А, являются базисными, а остальные — их ли­нейными комбинациями. Тогда эти (m — r) уравнений можно удалить из системы, причем в результате указанных элемен­тарных преобразований мы получаем эквивалентную систему:

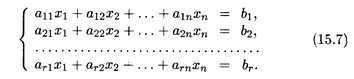
3. Система (15.7) характерна тем, что ее ранг равен числу уравнений в ней, причем r ≤ n, т.е. ранг не превосходит числа неизвестных. Поэтому возможны два случая: либо r = n, либо r < n. В первом случае система (15.7) имеет квадратную невырожденную матрицу порядка r (см. выше) и, согласно теореме Крамера, существует единственное решение этой системы. Иными словами, если ранг системы равен числу неизвестных, то система имеет единственное решение, т.е. она является оп­ределенной.

4. Рассмотрим теперь случай, когда r < п. Перенесем в правые части уравнений (15.7) все слагаемые, содержащие не­известные x_{r +1}, x_{r +2}, …, x_п. Тогда система принимает вид

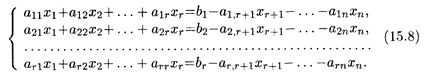
Неизвестным x_{r+ 1},..., x_п можно придавать любые значения, и потому они называются свободными. Неизвестные х ₁, x ₂,..., x_r соответствующие базисным столбцам, называются базисными. Из системы (15.8) легко найти выражения базисных неизвест­ных через свободные, согласно теореме Крамера, рассматри­вая правые части этих уравнений как элементы столбца сво­бодных членов, содержащие x_{r +1}, x_{r +2},…, х_п. Можно показать, что базисные неизвестные x ₁, х ₂,..., x_r линейно выражаются через свободные неизвестные. Поскольку свободные неизвест­ные могут принимать любые значения, то в случае когда ранг совместной системы меньше числа неизвестных, эта система является неопределенной: она имеет бесчисленное множество решений.

Дата добавления: 2014-10-15