Вычисление обратной матрицы методом Гаусса

Метод Гаусса является поистине универсальным в решении систем линейных алгебраических уравнений. Мы продемонст­рируем применение этого метода при вычислении обратных матриц.

Практически этот наиболее простой способ вычисления об­ратной матрицы состоит в следующих шагах.

1. К матрице А, по отношению к которой ищется обратная матрица, приписывается справа единичная матрица Е.

2. Путем преобразований методом Гаусса над строками рас­ширенной матрицы (А|Е) матрица А приводится к виду еди­ничной матрицы.

3. После окончания указанного вычислительного процесса, т.е. когда на месте исходной матрицы А будет сформирована единичная матрица, на месте приписанной справа единичной матрицы Е будет находиться обратная матрица А ^-1. Иными словами, вместо расширенной матрицы (А|Е) в итоге получaется расширенная матрица (E | A ^-1).

Продемонстрируем эту последовательность действий на не­сложном примере.

Пример 1. Найти обратную матрицу исходной матрицы

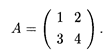
Решение. Выполняем последовательно шаги 1 — 3:

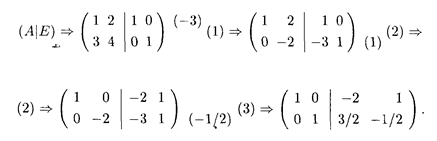
Схема вычислений по методу Гаусса пояснена здесь теми же обозначениями, что и в п. 15.2, при этом стрелками показано, к какой строке прибавляется измененная строка. Последний этап вычислений, показанный стрелкой (3), состоит в делении по­следней строки расширенной матрицы на -2. Итак, обратная матрица имеет вид

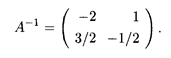
Нетрудно непосредственно проверить правильность прове­денных вычислений по определению обратной матрицы: АА ^-1 = А^{- 1} А.

Дата добавления: 2014-10-15