Фундаментальная система решений

Решения однородной системы обладают следующими свой­ствами. Если вектор 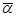= (α₁, α₂,...,α _n) является решением системы (15.14), то и для любого числа k вектор k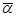= (kα ₁, kα ₂ ,..., kα_n) будет решением этой системы. Если решением сис­темы (15.14) является вектор 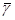= (γ₁, γ₂,...,γ _n), то сумма 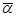+ 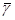также будет решением этой системы. Отсюда следует, что любая линейная комбинация решений однородной системы также является решением этой системы.

Как мы знаем из п. 12.2, всякая система n -мерных век­торов, состоящая более чем из п векторов, является линей­но зависимой. Таким образом, из множества векторов-решений однородной системы (15.14) можно выбрать базис, т.е. любой вектор-решение данной системы будет линейной комбинацией векторов этого базиса. Любой такой базис называется фунда­ментальной системой решений однородной системы линейных уравнений. Справедлива следующая теорема, которую мы при­водим без доказательства.

ТЕОРЕМА 4. Если ранг r системы однородных уравнений (15.14) меньше числа неизвестных п, то всякая фундамен­тальная система решений системы (15.14) состоит из п - r решений.

Укажем теперь способ нахождения фундаментальной сис­темы решений (ФСР). Пусть система однородных уравнений (15.14) имеет ранг r < п. Тогда, как следует из правил Краме­ра, базисные неизвестные этой системы x ₁, x ₂, … x_r линейно выражаются через свободные переменные x_{r+ 1}, x_{r+ 2},..., x_п:

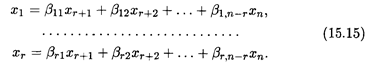
Выделим частные решения однородной системы (15.14) по сле­дующему принципу. Для нахождения первого вектора-решения 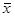₁ положим x_{r+ 1} = 1, x_{r+ 2} = x_r+3 =... = x_n = 0. Затем на­ходим второе решение 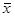₂: принимаем x_{r +2} = 1, а остальные r - 1 свободных переменных положим нулями. Иными словами, мы последовательно присваиваем каждой свободной перемен­ной единичное значение, положив остальные нулями. Таким образом, фундаментальная система решений в векторной фор­ме с учетом первых r базисных переменных (15.15) имеет вид

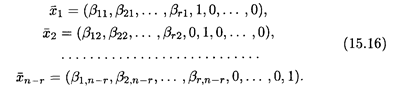
ФСР (15.16) является одним из фундаментальных наборов решений однородной системы (15.14).

Пример 1. Найти решение и ФСР системы однородных урав­нений

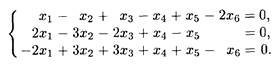
Решение. Будем решать эту систему методом Гаусса. По­скольку число уравнений системы меньше числа неизвестных, считаем х ₁, x ₂, х ₃ базисными неизвестными, а x ₄, х ₅, x ₆ — сво­бодными переменными. Составим расширенную матрицу сис­темы и выполним действия, составляющие прямой ход метода:

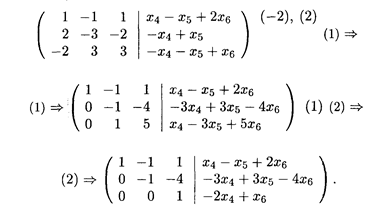
Преобразованная расширенная матрица соответствует системе уравнений, которая эквивалентна исходной однородной системе:

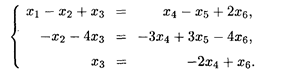
Обратный ход метода Гаусса дает значения базисных неиз­вестных, выраженные через свободные переменные:

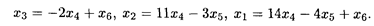
Поскольку ранг однородной системы равен трем, то ФСР для нее состоит из трех линейно независимых векторов. По фор­мулам (15.16) при п = 6 и r = 3, беря последовательно для свободных переменных тройки чисел (1, 0, 0), (0, 1, 0) и (0, 0, 1), получаем набор фундаментальных решений:

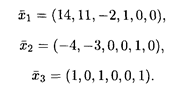
Дата добавления: 2014-10-15