Независимые события

Определение 3. Событие В называется независимым от со­бытия А, если условная вероятность события В равна его без­условной вероятности (появление события А не влияет на ве­роятность события В):

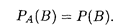
Отсюда следует, что и событие А также независимо от со­бытия В:

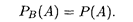
Для независимых событий теорема умножения вероятностей 17.3 в общей форме, которая следует из (17.6), имеет вид

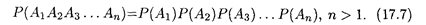
Равенство (17.7) принимается за определение независимых со­бытий. При этом если события независимы, то независимы также и соответствующие им противоположные события.

Пример 4. Найти вероятность поражения цели при совмест­ной стрельбе тремя орудиями, если вероятности поражения цели орудиями соответственно равны 0,9, 0,8 и 0,7 (события А, B и С).

Решение. Поскольку события А, В и С являются независимыми, то искомая вероятность вычисляется, согласно формуле (17.7), при n = 3:

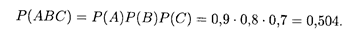
Когда в результате испытания может иметь место n неза­висимых событий с известными вероятностями их появления, особый интерес представляет случай нахождения вероятнос­ти наступления хотя бы одного из них (например, в случае трех событий найти вероятность наступления либо одного, ли­бо двух, либо трех событий). Обозначим это событие через А. Справедлива следующая теорема.

ТЕОРЕМА 4. Вероятность появления хотя бы одного из не­зависимых событий А₁, A₂,..., А_n определяется формулой

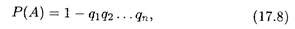
где q_i = 1 — p_i — вероятности соответствующих противо­положных событий 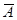_i (i = 1, 2,..., n).

В частном случае, когда все события Аi имеют одинаковую вероятность р, из формулы (17.8) следует, что

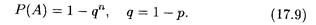
Пример 5. В условиях примера 4 найти вероятность пораже­ния цели (хотя бы одного попадания) при залповой стрельбе орудий.

Решение. Вероятности противоположных событий (про­махов) соответственно равны q ₁ = 0,1, q ₂ = 0,2, q ₃ = 0,3. Иско­мая вероятность находится по формуле (17.8) при п = 3:

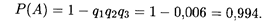
Из этого примера наглядно видно преимущество совместного воздействия случайных событий с целью достижения общего результата.

Пример 6. На перевозку груза направлены 4 автомобиля. Ве­роятность нахождения каждой из машин в исправном состоя­нии равна 0,8. Найти вероятность того, что в работе участвует хотя бы один из выделенных для этого автомобилей.

Решение. Вероятность противоположного события (маши­на неисправна) равна q = 1 - 0,8 = 0,2. По формуле (17.9) находим искомую вероятность при n = 4:

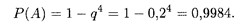
Пример 7. Вероятность обслуживания клиента одним опера­ционистом в банке равна 0,6. Какое минимальное число опе­рационистов должно работать в банке, чтобы вероятность об­служивания клиента была не менее 0,95?

Решение. Вероятность противоположного события (отказ в обслуживании клиента операционистом) равна 0,4. Пусть n — количество операционистов, удовлетворяющее условию за­дачи, т.е.

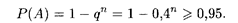
Решая это неравенство, получаем

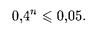
Логарифмирование обеих частей этого неравенства дает

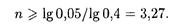
Поскольку n должно быть целым числом, окончательно получаем, что в банке должны работать не менее 4 операцио­нистов.

Дата добавления: 2014-10-15