Появление только одного из независимых событий

Обобщения теорем сложения и умножения

Рассмотрим примеры совместного применения теорем сло­жения и умножения. Пусть два независимых события А ₁ и А ₂имеют вероятности появления соответственно p ₁ и р ₂. Найдем вероятность появления только одного из этих событий. Для этого введем новые события: В ₁ и B ₂. Событие В ₁ состоит в том, что событие А ₁ наступило, а событие А ₂ не наступило; иными словами, В ₁ = A ₁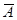₂. Аналогичным образом определя­ется и событие B ₂ = 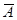₁ A ₂ (совместное ненаступление события A ₁ и наступление события А ₂). Поскольку события А ₁ и A ₂ независимы, то независимы также и противоположные coбытия 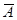₁ и 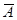₂; тогда события В ₁ и В ₂ являются несовместными. Вероятность наступления только одного из событий А ₁ и А ₂находится как сумма вероятностей несовместных событий В ₁ и B ₂:

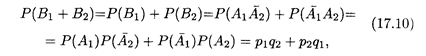
где _q1 = 1 – p ₁, q ₂ = 1 - р ₂.

Аналогичным образом можно убедиться в справедливости формулы вероятности наступления только одного из трех не­зависимых событий A ₁, А ₂, А ₃ с вероятностями наступления соответственно р ₁, р ₂и р ₃:

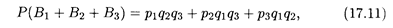
где B_i — произведения наступившего события А_i и двух дру­гих ненаступивших событий (i = 1, 2, 3). Для случая п неза­висимых событий формула вероятности наступления только одного из них имеет аналогичный вид — сумма п слагаемых, каждый член которой представляет собой произведение вероятности наступления одного из событий на вероятности (n - 1) других противоположных событий.

Пример 1. Предприниматель решил вложить свои средства поровну в два контракта, каждый из которых принесет ему прибыль в размере 100%. Вероятность того, что любой из кон­трактов не "лопнет", равна 0,8. Какова вероятность того, что по истечении контрактов предприниматель по меньшей мере ничего не потеряет?

Решение. Предприниматель по крайней мере ничего не по­теряет, если либо не "лопнет" один из контрактов (другой воз­местит ему потери), либо будут выполнены оба контракта. Пусть события А ₁ и А ₂ — это выполнение соответствующих контрактов (вероятность р = 0,8); эти события являются независимыми. Противоположные им события 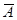₁ и 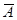₂ — не­выполнение контрактов (вероятность q = 0,2). Тогда собы­тия В ₁ = А ₁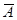₂, В ₂ = 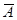₁ A ₂ и A ₁ A ₂ являются несовместны­ми (последнее событие — это выполнение обоих контрактов). Искомая вероятность определяется с учетом формул (17.10) и (17.7):

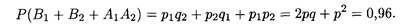
Дата добавления: 2014-10-15