Локальная теорема Лапласа

Использование формулы Бернулли (17.16) при больших значениях п и k представляется затруднительным ввиду уве­личения объема вычислений и операций с большими числами. В этом случае применима формула, устанавливаемая следую­щей локальной теоремой Лапласа.

ТЕОРЕМА 7. Пусть вероятность р появления события А в каждом испытании постоянна, причем 0 < р < 1. Тогда веро­ятность P_n(k) того, что событие А появится в п испытаниях ровно k раз, приближенно равна значению функции φ(x):

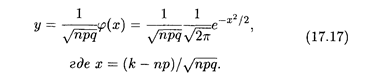
Точность формулы (17.17) возрастает с увеличением п. Имеются таблицы с вычисленными значениями функции φ(x) (см. Приложение), по которым можно с достаточно высокой степенью точности найти практически любое значение этой функции, а значит, и вычислить нужную вероятность. По­скольку функция φ (x) четная,то в таблицах даются ее значения только для положительных значений х; иными словами, знак аргумента не играет роли. Формула (17.17) носит название асимтотической формулы.

Пример 4. Вероятность выпуска бракованного изделия рав­на 0,3. Найти вероятность того, что среди 100 выпущенных изделий будет ровно 60 изделий без брака.

Решение. Вероятность появления события А в одном ис­пытании (изделие без брака) р = 0,7, тогда q = 0,3, в нашем случае п = 100, k = 60. Последовательно вычисляем:

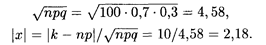
Теперь для найденного аргумента х находим по табл. 1 (см. Приложение) соответствующее значение φ (x); оно равно 0,0371. Подстановка этого числа в формулу (17.17) дает при­ближенное значение искомой вероятности:

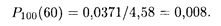
Дата добавления: 2014-10-15