Статистические оценки параметров распределения. Значения количественного признака х1, х2, , хk в выборке можно рассматривать как независимые случайные величины

Значения количественного признака х ₁, х ₂,..., х_k в выборке можно рассматривать как независимые случайные величины. В таком случае нахождение статистической оценки неизвест­ного параметра теоретического распределения означает отыс­кание функции от наблюдаемых случайных величин, которая и даст нам приближенное значение искомого параметра. Укажем виды статистических оценок.

Несмещенной называется статистическая оценка 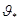, мате­матическое ожидание которой равно оцениваемому параметру 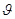при любой выборке:

Смещенной называется оценка, при которой условие (18.51) не выполнено. Эффективной называется оценка, которая имеет минимальную дисперсию при заданном объеме выборки п. Со­стоятельной называется статистическая оценка типа (18.50), которая при п > стремится по вероятности к оцениваемому параметру.

Теперь укажем виды числовых характеристик оценок. Прежде всего, это средние. Генеральная средняя для изучаемо­го количественного признака Х по генеральной совокупности

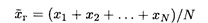
и выборочная средняя

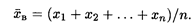
Если значения признака х ₁, x ₂, …, х_k в выборке имеют соответ­ственно частоты n ₁, n ₂,..., n_k, то последнюю формулу можно переписать в виде

Можно показать, что выборочная средняя (18.52) является не­смещенной оценкой; это аналог математического ожидания случайной величины.

Введем в рассмотрение величины, характеризующие от­клонение значений количественного признака Х от своего сред­него значения. Это генеральная дисперсия:

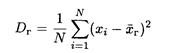
и выборочная дисперсия:

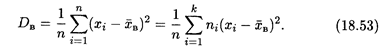
Можно показать, что для вычисления этих характеристик справедливы более удобные формулы, аналогичные дисперсии случайной величины; так, формула (18.53) принимает вид

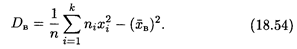
Генеральное среднее квадратическое отклонение опреде­ляется как

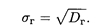
Аналогично вводится и выборочное среднее квадратическое отклонение

Пример 4. Выборка задана таблицей распределения

Найти выборочные характеристики: среднюю, дисперсию и среднее квадратическое отклонение.

Решение. По формуле (18.52) сначала находим 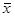_в:

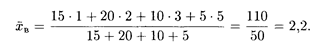
Затем по формулам (18.54) и (18.55) находим две другие иско­мые величины:

Дата добавления: 2014-10-15