УПРАЖНЕНИЯ. 18.1. Из коробки с шестью деталями, среди которых четыре стандартные, наудачу взяты три детали

18.1. Из коробки с шестью деталями, среди которых четыре стандартные, наудачу взяты три детали. Составить закон рас­пределения дискретной случайной величины Х — количества стандартных деталей среди отобранных.

18.2. Книга издана тиражом 100 тысяч экземпляров. Вероят­ность брака в книге равна 0,0001. Найти вероятность того, что тираж содержит ровно 5 бракованных книг.

18.3. Случайная составляющая дохода равна 2 Х, а случайная составляющая затрат равна 50 Y. Найти дисперсию прибыли при условиях: величина Х распределена по биномиальному за­кону с параметрами п = 100, р = 0,5; величина Y распределена по закону Пуассона с параметром λ = 2; случайные величины Х и Y являются независимыми.

18.4. Найти дисперсию и среднее квадратическое отклонение случайной величины X, заданной законом распределения

18.5. Найти дисперсию дискретной случайной величины Х — числа отказов элемента некоторого устройства — в 10 неза­висимых опытах, если вероятность отказа элемента в каждом опыте равна 0,9.

18.6. Дискретная случайная величина Х задана законом рас­пределения

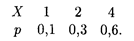
Найти центральные моменты первого, второго, третьего и чет­вертого порядков.

18.7. Дано распределение двумерной дискретной случайной ве­личины (X, Y):

Найти ковариацию Cov (X, Y) и коэффициент корреляции Х и Y.

18.8. Непрерывная случайная величина Х задана на всей оси Ох функцией распределения F (x) = 1/2 + (arctg x) / π. Найти вероятность того, что величина Х примет значение, заключен­ное в интервале (0, 1).

18.9. Случайная величина Х задана функцией распределения

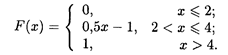
Найти вероятность того, что Х примет значения: а) менее 0,2; б) менее трех; в) не менее трех; г) не менее пяти.

18.10. Дискретная случайная величина задана законом распре­деления

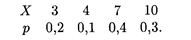
Найти функцию распределения и построить ее график.

18.11. Дана плотность распределения непрерывной случайной величины X:

Найти функцию распределения F(x).

18.12. Случайная величина Х задана на положительной полу­оси Ох функцией распределения F(x) = 1 - e^-ax (а > 0). Найти математическое ожидание величины X.

18.13. Случайная величина Х задана на интервале (0,5) плот­ностью распределения f(x) = 2. x / 25; вне этого интервала f (x) = 0. Найти дисперсию X.

18.14. Случайная величина Х задана плотностью распределе­ния f (x) = е^-|x| / 2. Найти математическое ожидание и диспер­сию.

18.15. Случайная величина задана функцией распределения

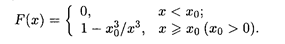
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.

18.16. Найти дисперсию и среднее квадратическое отклонение случайной величины X, распределенной равномерно в интер­вале (2, 8).

18.17. Ребро куба х измерено приближенно в интервале (а, b). Найти математическое ожидание и дисперсию объема куба, ес­ли его ребро рассматривать как случайную величину Х с рав­номерным распределением на указанном интервале.

18.18. Размер мужских сорочек является случайной величиной с нормальным законом распределения, математическим ожи­данием 39 и дисперсией 9. Какой процент от общего объема заказа следует предусмотреть магазину для сорочек 40-го раз­мера воротничка при условии, что этот размер находится в интервале (39,5; 40,5)?

18.19. Найти формулу плотности вероятности нормально рас­пределенной случайной величины X, если математическое ожидание равно 3, а дисперсия равна 16.

18.20. Случайная величина Х распределена нормально с ма­тематическим ожиданием а = 25. Вероятность попадания Х в интервал (10, 15) равна 0,2. Найти вероятность попадания Х в интервал (35, 40).

Раздел II. ОСНОВЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ

Управление и планирование являются наиболее сложными функциями в работе предприятий, фирм, служб администра­ций всех уровней. Долгое время они являлись монополией че­ловека с соответствующей подготовкой и опытом работы. Со­вершенствование науки, техники, разделение труда усложнили принятие решений в управлении и планировании.

Для принятия обоснованного решения необходимо иметь и обработать большое количество информации, определяемое иногда астрономическими цифрами. Принятие ответственных решений, как правило, связано с большими материальными ценностями. В настоящее время недостаточно знать путь, ве­дущий к достижению цели. Необходимо из всех возможных пу­тей выбрать наиболее экономичный, который наилучшим об­разом соответствует поставленной задаче.

Появление цифровых вычислительных машин и персональ­ных компьютеров создало огромные возможности для разви­тия науки, совершенствования методов планирования и управ­ления производством. Однако без строгих формулировок задач, без математического описания процессов современный уровень управления и планирования не может быть достигнут.

Задачи управления и планирования обычно сводятся к вы­бору некоторой системы параметров и системы функций, ко­торые приводят к экстремальным задачам следующего вида.

Требуется найти максимум функции

при условиях:

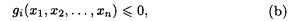
где f, g_i — функции, x ₁, x ₂,..., x_п — параметры управления.

Выражение (а) называется функцией цели. Условия (b) и (с) представляют собой ограничения поставленной задачи. Усло­вия (с) справедливы для многих задач, особенно экономичес­ких, когда параметры управления (x_j) по своему физическом смыслу не могут быть отрицательными. Среди условий задачи могут быть равенства.

Математическая дисциплина, занимающаяся изучением эк­стремальных (максимальных или минимальных) задач управ­ления, планирования и разработкой методов их решения, полу­чила название математического программирования.

Основное отличие задач математического программирова­ния от условных экстремальных задач, рассмотренных в час­ти 6, заключается в наличии неравенств в системе ограниче­ний. Поэтому методы решения задач на условный экстремум с помощью множителей Лагранжа не могут быть применены.

В зависимости от вида функции цели и ограничений ма­тематическое программирование делится на линейное и нели­нейное.

Наиболее разработанным разделом математического про­граммирования является линейное программирование.

В задачах линейного программирования возможны случаи, когда параметры управления могут принимать лишь целые дискретные значения. При решении подобных задач использу­ется целочисленное программирование.

В некоторых случаях исходные параметры задачи могут изменяться в некоторых пределах, для их решения применяет­ся параметрическое программирование.

В настоящее время не существует общих и достаточно эф­фективных методов решения задач нелинейного программи­рования. Лишь для определенного класса нелинейных задач, система ограничений которых линейна, а целевая функция не­линейна, но обладает свойством выпуклости, разработаны до­статочно эффективные методы, получившие название методов выпуклого программирования.

На практике часто приходится сталкиваться с ситуациями, в которых необходимо принимать решения при наличии двух или более сторон, имеющих различные цели. Результаты любого действия каждой из сторон зависят от решений партнеров. В экономике подобные ситуации встречаются довольно часто. Для решения задач с конфликтными ситуациями используют математические методы теории игр.

Динамическое программирование — один из разделов ме­тодов оптимизации, в котором процесс принятия решения мо­жет быть разбит на отдельные этапы. В основе метода лежит принцип оптимальности, разработанный Р. Беллманом.

Сетевые модели, в основе которых лежит теория графов, позволяют проводить их оптимизацию, а также совокупность расчетных и организационных мероприятий по управлению комплексами работ при создании новых изделий и технологий.

Цель изучения системы массового обслуживания состоит в том, чтобы контролировать их характеристики для проведения оптимизации системы в целом.

Рассмотрение моделей управления запасами преследует цель выбора для предприятий оптимальных расходов на до­ставку, хранение комплектующих материалов и ресурсов, не­обходимых для изготовления изделий.

Дата добавления: 2014-10-15