Виды дисперсий

Часто значения количественного признака Х совокупности разбиваются на определенное число групп. Каждую группу можно рассматривать как самостоятельную выборку, и для каждой группы можно определить групповую среднюю и дис­персию. Пусть r — число групп. Групповой дисперсией на зывается дисперсия значений признака в группе относительно групповой средней:

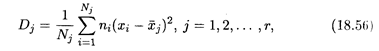
где n_i — частота значения x_i в группе, j — номер группы 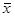_j — групповая средняя j- й группы, N_j = 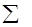n_i, — объем j -й группы.

Зная дисперсию каждой группы, можно определить их сред­нюю арифметическую. Внутригрупповой дисперсией называ­ется средняя арифметическая дисперсий, где каждое слагаемое входит с весом объема группы:

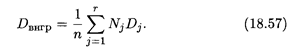
В свою очередь, зная для всех групп средние 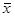_j и общую среднюю 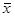, введем еще одно понятие. Межгрупповой диспер­сией называется дисперсия групповых средних относительно общей средней:

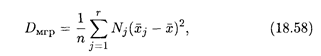
где п = 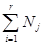— объем всей совокупности.

Для общей дисперсии всей совокупности справедлива сле­дующая теорема, которая приводится здесь без доказатель­ства.

ТЕОРЕМА 6. Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий:

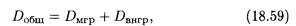
где слагаемые в правой части определяются соответствен­но формулами (18.57) и (18.58).

Поясним сказанное в этом пункте на примере.

Пример 5. Совокупность состоит из двух следующих групп:

Найти групповые, внутригрупповую, межгрупповую и общую дисперсии.

Решение. Объемы групп соответственно равны N ₁ = 10 и N ₂ = 5. Общий объем совокупности: п = 10 + 5 = 15. Найдем групповые средние:

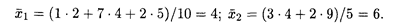
Теперь находим групповые дисперсии по формуле (18.56):

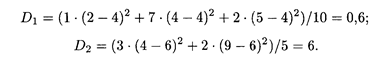
Внутригрупповая дисперсия, согласно формуле (18.57), равна:

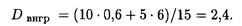
Теперь найдем межгрупповую дисперсию по формуле (18.58), для чего сначала определим общую среднюю:

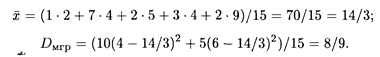
Наконец, общая дисперсия, согласно формуле (18.59), равна:

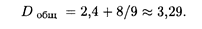
Дата добавления: 2014-10-15