Основные понятия и определения

Дано n -мерное пространство, точки которого имеют коор­динаты (x ₁, x ₂,... ,x_п).

Определение 1. Множество точек n -мерного пространства, координаты которых удовлетворяют уравнению

где хотя бы одно из чисел а ₁, a ₂,..., a_n отлично от нуля, на­зывается гиперплоскостью п-мерного пространства.

В векторной форме оно записывается следующим образом:

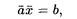
где = (a ₁, a ₂,..., a_n), = (x ₁, x ₂,..., x_n).

Даны две гиперплоскости

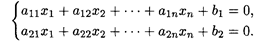
Определение 2. Множество точек n -мерного пространства, координаты которых одновременно удовлетворяют каждому уравнению системы, называется пересечением гиперплоскос­тей.

Дано неравенство

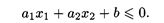
Эта зависимость определяет полуплоскость двухмерного про­странства, лежащую по одну сторону от прямой

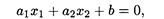
которая называется граничной прямой.

Определение 3. Множество точек n -мерного пространства, координаты которых удовлетворяют неравенству

называется полупространством n -мерного пространства, рас­положенным по одну сторону от гиперплоскости

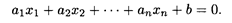
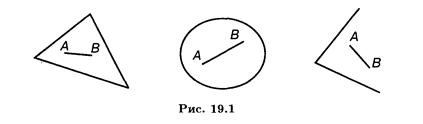
Определение 4. Множество точек n -мерного пространства, содержащее вместе с любыми двумя точками A и В и все точ­ки отрезка АВ, называется выпуклым телом (областью, фи­гурой).

Примеры плоских выпуклых фигур приведены на рис. 19.1.

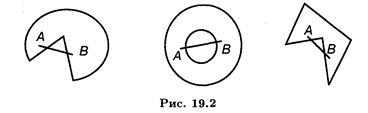
Примеры невыпуклых фигур приведены на рис. 19.2.

Дадим некоторые определения выпуклой области.

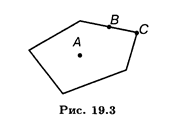
Определение 5. Точка А называется внутренней точкой вы­пуклой области, если в сколь угодно малой окрестности этой точки содержатся только точки этой области.

Определение 6. Точка В называется граничной точкой вы­пуклой области, если в сколь угодно малой окрестности этой точки содержатся как точки данной области, так и не принад­лежащие ей (рис. 19.3).

Определение 7. Точка С называется угловой точкой вы­пуклой области, если она является граничной и не лежит внутри отрезка, соединяющего две другие точки этой облас­ти (рис. 19.3).

Определение 8. Если область включает все свои граничные точки, то она называется замкнутой.

Выпуклая область может быть ограниченной и неограни­ченной.

Определение 9. Ограниченной называется область, если су­ществует такое число М > 0, что радиус-вектор, соединяю­щий начало координат с любой точкой области, по абсолютной величине меньше М, т.е. || ≤ М.

Для этой области все ее точки находятся на конечном рас­стоянии от начала координат.

Определение 10. Если найдутся точки области, сколь угод­но удаленные от начала координат, то область называется не­ограниченной.

Определение 11. Выпуклая замкнутая ограниченная область, имеющая конечное число угловых точек, называется вы­пуклым п-мерным многогранником.

Определение 12. Выпуклая замкнутая неограниченная об­ласть, имеющая конечное число угловых точек, называется вы­пуклой п-мерной многогранной областью.

Определение 13. Линейная комбинация S векторов

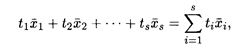
в которой коэффициенты t_i удовлетворяют условиям

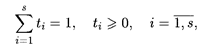
называется выпуклой линейной комбинацией.

Определение 14. Пересечением выпуклых областей называ­ется множество точек, являющееся общей частью этих облас­тей.

ТЕОРЕМА 1. Пересечение выпуклых областей есть выпуклая область.

ТЕОРЕМА 2. Множество точек выпуклого п-мерного много­гранника совпадает с множеством любых выпуклых линейных комбинаций его угловых точек.

19.2. Решение систем m линейных неравенств с двумя переменными

Дана система т линейных неравенств с двумя переменными

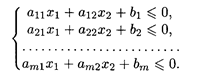
Знаки некоторых или всех неравенств могут быть ≥.

Рассмотрим первое неравенство в системе координат Х ₁ ОХ ₂. Построим прямую

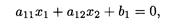
которая является граничной прямой.

Эта прямая делит плоскость на две полуплоскости 1 и 2 (рис. 19.4).

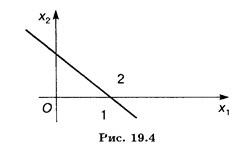
Полуплоскость 1 содержит начало координат, полуплос­кость 2 не содержит начала координат.

Для определения, по какую сторону от граничной прямой расположена заданная полуплоскость, надо взять произволь­ную точку на плоскости (лучше начало координат) и подста­вить координаты этой точки в неравенство. Если неравенство справедливо, то полуплоскость обращена в сторону этой точки, если не справедливо, то в противоположную от точки сторону.

Направление полуплоскости на рисунках показываем стрел­кой.

Определение 15. Решением каждого неравенства систе­мы является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее.

Определение 16. Пересечение полуплоскостей, каждая из ко­торых определяется соответствующим неравенством системы, называется областью решения системы (ОР).

Определение 17. Область решения системы, удовлетворяю­щая условиям неотрицательности (x_j ≥ 0, j =), называ­ется областью неотрицательных, или допустимых, решений (ОДР).

Если система неравенств совместна, то ОР и ОДР могут быть многогранником, неограниченной многогранной облас­тью или одной точкой.

Если система неравенств несовместна, то ОР и ОДР — пус­тое множество.

Пример 1. Найти ОР и ОДР системы неравенств и опреде­лить координаты угловых точек ОДР

Решение. Найдем ОР первого неравенства: х ₁ + 3 x ₂ ≥ 3. Построим граничную прямую х ₁ +3 x ₂ – 3 = 0 (рис. 19.5). Под­ставим координаты точки (0,0) в неравенство: 1∙0 + 3∙0 > 3; так как координаты точки (0,0) не удовлетворяют ему, то решени­ем неравенства (19.1) является полуплоскость, не содержащая точку (0,0).

Аналогично найдем решения остальных неравенств систе­мы. Получим, что ОР и ОДР системы неравенств является выпуклый многогранник ABCD.

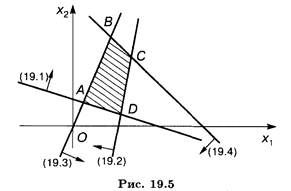
Найдем угловые точки многогранника. Точку А определим как точку пересечения прямых

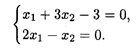
Решая систему, получим А (3/7, 6/7).

Точку В найдем как точку пересечения прямых

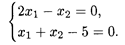
Из системы получим B (5/3, 10/3). Аналогично найдем коорди­наты точек С и D: С (11/4; 9/14), D (3/10; 21/10).

Пример 2. Найти ОР и ОДР системы неравенств

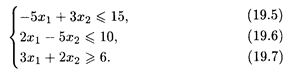
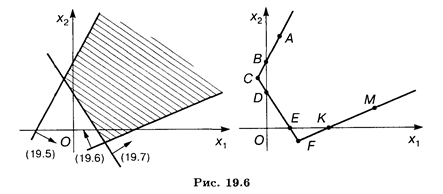
Решение. Построим прямые и определим решения не­равенств (19.5)-(19.7). ОР и ОДР являются неограниченные многогранные области ACFM и ABDEKM соответственно (рис. 19.6).

Пример 3. Найти ОР и ОДР системы неравенств

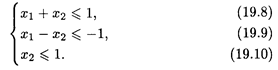
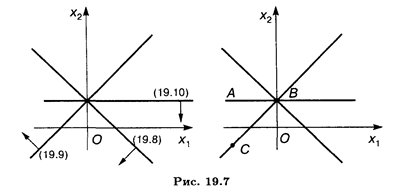
Решение. Найдем решения неравенств (19.8)-(19.10) (рис. 19.7). ОР представляет неограниченную многогранную область ABC; ОДР — точка В.

Пример 4. Найти OP и ОДР системы неравенств

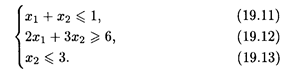
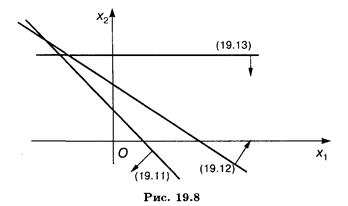
Решение. Построив прямые, найдем решения неравенств системы. ОР и ОДР несовместны (рис. 19.8).

Дата добавления: 2014-10-15