Экономический анализ задач с использованием теории двойственности

Рассмотрим задачу оптимального использования ресурсов, запишем ее математическую модель

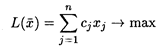
при ограничениях:

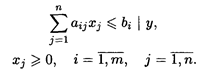
Двойственная задача имеет вид

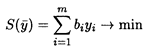
при ограничениях:

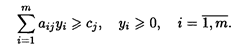
ТЕОРЕМА 3. Значения переменных у_i в оптимальном реше­нии двойственной задачи представляют собой оценки влия­ния свободных членов системы ограничений исходной задачи на оптимальное значение ее целевой функции, т.е.

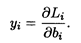
Примем 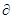L_i ≈ ΔL_i, 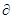b_i ≈ Δb_i, тогда ΔL_i ≈ y_i • Δb_i.

Для задачи оптимального использования сырья это уравне­ние показывает, что при изменении i -го ресурса оптимальный доход является линейной функцией от его приращения, причем коэффициентом служит у_i — i-я компонента оптимального ре­шения двойственной задачи.

Если y_i мало, то значительному увеличению i -го ресур­са будет соответствовать небольшое увеличение оптимального дохода и ценность ресурса невелика.

Если y_i = 0, то при увеличении i -го ресурса оптимальный доход остается неизменным и ценность этого ресурса равна нулю. В самом деле, сырье, запасы которого превышают по­требности в нем, не представляет ценности для производства и его оценку можно принять за нуль.

Если у_i велико, то незначительному увеличению i -го ресур­са будет соответствовать существенное увеличение оптималь­ного дохода и ценность ресурса высока. Уменьшение ресурса ведет к существенному сокращению выпуска продукции.

Переменную у_i считают некоторой характеристикой цен­ности i -го ресурса. В частности, при увеличении i -го ресурса на единицу (Δb_i = 1) оптимальный доход возрастает на y_i, что позволяет рассматривать y_i как "условную цену", оценку единицы i -го ресурса, объективно обусловленную оценку.

Так как у_i представляет частную производную от опти­мального дохода по i -му ресурсу, то у_i характеризует скорость изменения оптимального дохода при изменении i -го ресурса.

С помощью y_i можно определить степень влияния огра­ничений на значение целевой функции. Предельные значения (нижняя и верхняя границы) ограничений ресурсов, для кото­рых y_i остаются неизменными, определяются по формулам:

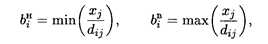
где x_j — значение переменной в оптимальном решении; d_ij — элементы матрицы (d_ij) = А ^-1, обратной к матрице базиса оптимального решения, для которой А = (a_ij)_{m x n} .

Если в план включаются новые виды продукции, то их оценка находится по формуле

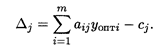
Если Δ _j < 0, то новый вид продукции улучшает план. При Δ _j > 0 нецелесообразно включать новый вид продукции.

Дата добавления: 2014-10-15