Альтернативный оптимум

При решении задач линейного программирования сим­плексным методом критерием оптимальности является условие Δ _j ≥ 0 для задач на максимум и условие Δ _j < 0 для задач на минимум. Если на каком-то шаге окажется, что хотя бы одна оценка свободной переменной Δ _j = 0, а все остальные Δ _j > 0 для задач на максимум (Δ _j < 0 для задач на минимум), то, приняв в качестве ключевого столбца столбец, где Δ _j = 0, и найдя новое оптимальное решение, заметим, что значение це­левой функции при этом не изменится. Говорят, что в этом случае задача имеет альтернативный оптимум.

Критерием альтернативного оптимума при решении за­дач симплексным методом является равенство нулю хотя бы одной оценки свободной переменной (Δ _j = 0).

Если только одна оценка свободной переменной равна ну­лю, то решение находится по формуле

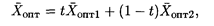
где 0 ≤ t ≤ 1.

Если две оценки и более, например S, свободных перемен­ных равны нулю, то оптимальное решение определяется по формуле

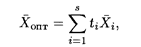
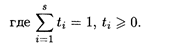
В задачах, имеющих альтернативный оптимум, возникает возможность включения в ее модель других критериев эффек­тивности.

Пример. Дана задача линейного программирования

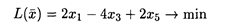
при ограничениях:

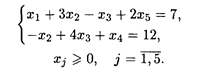
Решение. Составим симплексную таблицу (табл. 21.6).

В индексной строке имеется одна положительная оцен­ка. Полученное решение можно улучшить. Ключевым элемен­том является (4). Составляем симплексную таблицу 2-го шага (табл. 21.7).

Получаем

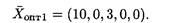
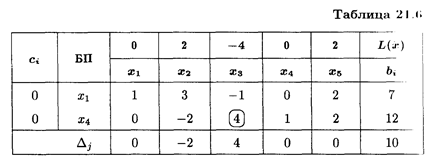
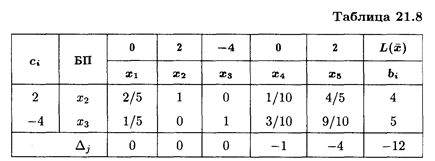
Так как Δ₂ = 0, то задача имеет альтернативный оптимум. Найдем еще одно оптимальное решение, введя вместо базисной переменной х ₁ свободную переменную х ₂ (табл. 21.8).

Получаем

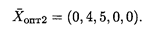
Найдем координаты оптимального решения задачи:

Давая t значения из [0,1], получим различные _опт, при кото­рых L() = -12.

Дата добавления: 2014-10-15