УПРАЖНЕНИЯ. Решить следующие задачи симплексным методом

Решить следующие задачи симплексным методом.

21.1. L() = x ₁ — 3 x ₂ — 5 x ₃ — х ₄ → max при ограничениях:

21.2. L() = x ₁ + 2 x ₂ + 3 x ₃ → min при ограничениях:

21.3. L() = —2 x ₁ — x ₂ + x ₃ + x ₄ → max при ограничениях:

21.4. L() = 3 x ₁ + x ₂ + 2 x ₃ → min при ограничениях:

21.5. L() = x ₁ + х ₂ + x ₃ → max при ограничениях:

21.6. L() = x ₁ + 2 х ₂ + 2 х ₃ → min при ограничениях:

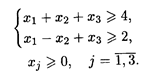
21.7. L() = 3 x ₁ + x ₂ + x ₃ + x ₄ → max при ограничениях:

21.8. L() = x ₁ - 5 x ₂ – x ₃ → max при ограничениях:

21.9. L() = x ₁ + х ₂ + x ₃ + x ₄ → min при ограничениях:

21.10. L() = 3 x ₁ + 5 x ₂ + 4 x ₃ → max при ограничениях:

21.11. Механический завод при изготовлении двух типов дета­лей использует токарное, фрезерное и сварочное оборудование. При этом обработку каждой детали можно вести двумя раз­личными технологическими способами. Необходимые исход­ные данные приведены в табл. 21.9.

Составить оптимальный план загрузки оборудования, обес­печивающий заводу максимальную прибыль.

21.12. Торговая фирма для продажи товаров трех видов ис­пользует ресурсы: время и площадь торговых залов. Затраты ресурсов на продажу одной партии товаров каждого вида да­ны в табл. 21.10. Прибыль, получаемая от реализации одной партии товаров 1-го вида, — 5 усл. ед., 2-го вида — 8 усл. ед., 3-го вида — 6 усл. ед.

Определить оптимальную структуру товарооборота, обес­печивающую фирме максимальную прибыль.

21.13. Фирма выпускает четыре пользующихся спросом изде­лия, причем месячная программа выпуска составляет 10 изде­лий типа 1 и 3, 200 изделий типа 2 и 120 изделий типа 4. Нормы затрат сырья на единицу различных типов изделий приведены в табл. 21.11.

Прибыль от реализации изделий типа 1 равна 6 усл. ед., изделий типа 2 — 2 усл. ед., изделий типа 3 — 2,5 усл. ед. и изделий типа 4 — 4 усл. ед.

Определить, является ли месячная программа выпуска из­делий оптимальной, и если нет, то определить оптимальную месячную программу и дополнительный доход, который фир­ма может при этом получить.

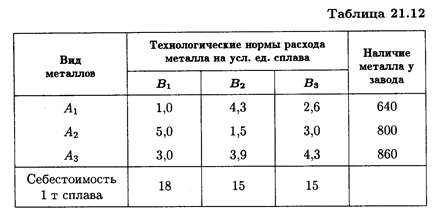
21.14. Металлургический завод из металлов A ₁, A ₂, А ₃ может выпускать сплавы B ₁, В ₂, В ₃. В течение планируемого пери­ода завод должен освоить не менее 640 т металла A ₁ и 800 т металла А ₂, при этом металла А ₃ может быть израсходовано не более 860 т.

Определить минимальные затраты, если данные о нормах расхода и себестоимость даны в табл. 21.12.

21.15. Ткань трех артикулов производится на ткацких станках двух типов с различной производительностью. Для изготов­ления ткани используются пряжа и красители. В табл. 21.13 указаны мощности станков в тысячах станко-часов, ресурсы пряжи и красителей в 1000 кг, производительности станков в метрах за час, нормы расхода пряжи и краски в килограммах на 1000 м и цена 1 м ткани.

По этим исходным данным решить следующие задачи:

1) определить оптимальный ассортимент, максимизирую­щий товарную продукцию предприятия;

2) приняв условие, что количество тканей трех артикулов находится в отношении 2:1:3, определить, какое мак­симальное количество комплектов ткани может выпус­тить предприятие;

3) определить оптимальный ассортимент, максимизирую­щий доход предприятия, если цена 1 м ткани составляет 8, 5 и 15 усл. ед. соответственно;

4) решить задачу (1) при условии, что станки 1-го типа ткань первого артикула не производят.

Глава 22. ДВОЙСТВЕННОСТЬ В ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ

Произвольную задачу линейного программирования можно определенным образом сопоставить с другой задачей линей­ного программирования, называемой двойственной. Первона­чальная задача является исходной. Эти две задачи тесно свя­заны между собой и образуют единую двойственную пару.

Различают симметричные, несимметричные и смешанные двойственные задачи.

Дата добавления: 2014-10-15