
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Электростатическое поле в вакууме
|
|
|
|
Точечный заряд +q находится в центре сферической поверхности. Если увеличить радиус сферической поверхности, то поток вектора напряженности электростатического поля  через поверхность сферы…
через поверхность сферы…
1) не изменится
2) увеличится
3) уменьшится
Решение:
Поток вектора напряженности сквозь сферическую поверхность радиуса 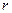 , охватывающую точечный заряд , охватывающую точечный заряд  , находящийся в центре, равен , находящийся в центре, равен  , т.е. не зависит от радиуса сферической поверхности, а зависит только от величины заряда.
Ответ: вариант 1. , т.е. не зависит от радиуса сферической поверхности, а зависит только от величины заряда.
Ответ: вариант 1.
|
Точечный заряд +q находится в центре сферической поверхности. Если добавить заряд –q внутрь сферы, то поток вектора напряженности электростатического поля  через поверхность сферы…
через поверхность сферы…
1) не изменится
2) увеличится
3) уменьшится
4) станет равным нулю
Решение:
Поток вектора напряженности электростатического поля сквозь сферическую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на  . .
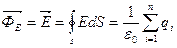 (1). Добавление отрицательного заряда внутрь сферы приводит к уменьшению вектора напряженности электростатического поля через поверхность т.к. векторы напряженности полей, создаваемые зарядами, имеют противоположные курсы.
Ответ: вариант 3. (1). Добавление отрицательного заряда внутрь сферы приводит к уменьшению вектора напряженности электростатического поля через поверхность т.к. векторы напряженности полей, создаваемые зарядами, имеют противоположные курсы.
Ответ: вариант 3.
|
Поле создано бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда  . Укажите направление вектора градиента потенциала в точке А.
. Укажите направление вектора градиента потенциала в точке А.

1) А – 4 2) А – 2 3) А – 3 4) А – 1
Решение:
Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее обе стороны. Напряженность поля равна градиенту потенциала со знаком минус ( ). Знак минус определяется тем, что вектор напряженности поля направлен в сторону убывания потенциала.
Ответ: вариант 1. ). Знак минус определяется тем, что вектор напряженности поля направлен в сторону убывания потенциала.
Ответ: вариант 1.
|
В некоторой области пространства создано электростатическое поле, потенциал которого описан функцией  . Вектор напряженности электрического поля в точке пространства, показанной на рисунке, имеет направление…
. Вектор напряженности электрического поля в точке пространства, показанной на рисунке, имеет направление…

1) 4 2) 1 3) 2 4) 3
Решение:
 Ответ: вариант 1.
Ответ: вариант 1.
|
Сила взаимодействия двух отрицательных точечных зарядов, находящихся на расстоянии R друг от друга, равна F. Знаки зарядов обеих частиц изменили на противоположные. Чтобы сила взаимодействия F не изменилась, расстояние между зарядами надо …
1) уменьшить в 2 раза
2) оставить без изменения
3) увеличить в 4 раза
4) уменьшить в 
Решение:
Согласно закону Кулона сила взаимодействия между двумя неподвижными точечными зарядами пропорциональна зарядам и обратно пропорциональна квадрату расстояния между ними:
 (1),
где (1),
где  ( (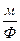 ) - коэффициент пропорциональности, ) - коэффициент пропорциональности,  ( (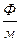 )
Как видно из выражения (1) заряды )
Как видно из выражения (1) заряды 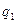 и и  взяты по модулю, что означает, величина силы от знака зарядов не зависит. Следовательно, изменяя знаки зарядов на противоположные, не следует изменить расстояние между ними для сохранения величину силы взаимодействия.
Ответ: вариант 2. взяты по модулю, что означает, величина силы от знака зарядов не зависит. Следовательно, изменяя знаки зарядов на противоположные, не следует изменить расстояние между ними для сохранения величину силы взаимодействия.
Ответ: вариант 2.
|
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 11311; Нарушение авторских прав?; Мы поможем в написании вашей работы!