
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Молекул
|
|
|
|
Число степеней свободы и средняя энергия
Средняя кинетическая энергия молекул газа при температуре Т зависит от их структуры, что связано с возможностью различных видов движения атомов в молекуле. Средняя кинетическая энергия молекул гелия (He) равна …
1) 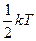 2)
2) 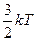 3)
3) 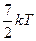 4)
4) 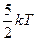
Решение:
Средняя кинетическая энергия молекул газа определяется соотношением 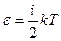 , где , где 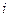 - сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы, т.е. число независимых переменных (координат), полностью определяющих положение системы в пространстве: - сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы, т.е. число независимых переменных (координат), полностью определяющих положение системы в пространстве:
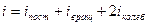 (1) (1)
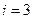 - для молекул одноатомного газа, которую рассматривают как материальную точку, которой приписывают три степени свободы поступательного движения. - для молекул одноатомного газа, которую рассматривают как материальную точку, которой приписывают три степени свободы поступательного движения.
 - для молекул двухатомного газа, которые кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения вокруг каждой из них. - для молекул двухатомного газа, которые кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения вокруг каждой из них.
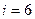 - для молекул газа состоящих из трех и более атомов: три поступательного и три вращательного движения.
В отличие от идеального газа для молекул реальных газов необходимо учитывать степени свободы колебательного движения. Поскольку между молекулами реального газа не существует жесткой связи. В нашем случае гелий является одноатомным газом и для его молекул число степеней свободы равно 3.
Ответ: вариант 2. - для молекул газа состоящих из трех и более атомов: три поступательного и три вращательного движения.
В отличие от идеального газа для молекул реальных газов необходимо учитывать степени свободы колебательного движения. Поскольку между молекулами реального газа не существует жесткой связи. В нашем случае гелий является одноатомным газом и для его молекул число степеней свободы равно 3.
Ответ: вариант 2.
|
Средняя кинетическая энергия молекулы идеального газа при температуре T равна 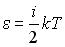 . Здесь
. Здесь 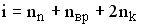 , где
, где 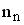 ,
, 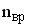 и
и 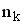 – число степеней свободы поступательного, вращательного и колебательного движений молекулы. Для атомарного водорода число i равно …
– число степеней свободы поступательного, вращательного и колебательного движений молекулы. Для атомарного водорода число i равно …
1) 1 2) 5 3) 7 4) 3
| Решение: У атомарного водорода молекулы состоят из одного атома. Поэтому его молекулы обладают числом степеней свободы равное 3. Ответ: вариант 4. |
Средняя кинетическая энергия молекулы идеального газа при температуре T равна 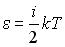 . Здесь
. Здесь 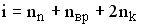 , где
, где 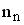 ,
, 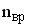 и
и 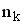 – число степеней свободы поступательного, вращательного и колебательного движений молекулы. При условии, что имеют место только поступательное и вращательное движение, для водорода (Н2) число i равно …
– число степеней свободы поступательного, вращательного и колебательного движений молекулы. При условии, что имеют место только поступательное и вращательное движение, для водорода (Н2) число i равно …
1) 7 2) 5 3) 2 4) 8
| Решение: По условию задачи имеет место, водород молекулы которого состоят из двух атомов. Для двухатомного газа число степеней свободы составляет 5. Ответ: вариант 2. |
Средняя кинетическая энергия молекулы идеального газа при температуре T равна 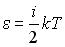 . Здесь
. Здесь 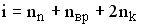 , где
, где 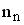 ,
, 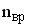 и
и 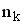 – число степеней свободы поступательного, вращательного и колебательного движений молекулы. При условии, что имеют место только поступательное и вращательное движение, для водяного пара (Н2O) число i равно …
– число степеней свободы поступательного, вращательного и колебательного движений молекулы. При условии, что имеют место только поступательное и вращательное движение, для водяного пара (Н2O) число i равно …
1) 8 2) 6 3) 3 4) 5
| Решение: По условию задачи имеет место, водяной пар, молекулы которого состоят из двух атомов водорода и одного атома кислорода. В сумме дают число 3. Для трехатомных молекул газа число степеней свободы равно 6. Ответ: вариант 2. |
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 13107; Нарушение авторских прав?; Мы поможем в написании вашей работы!